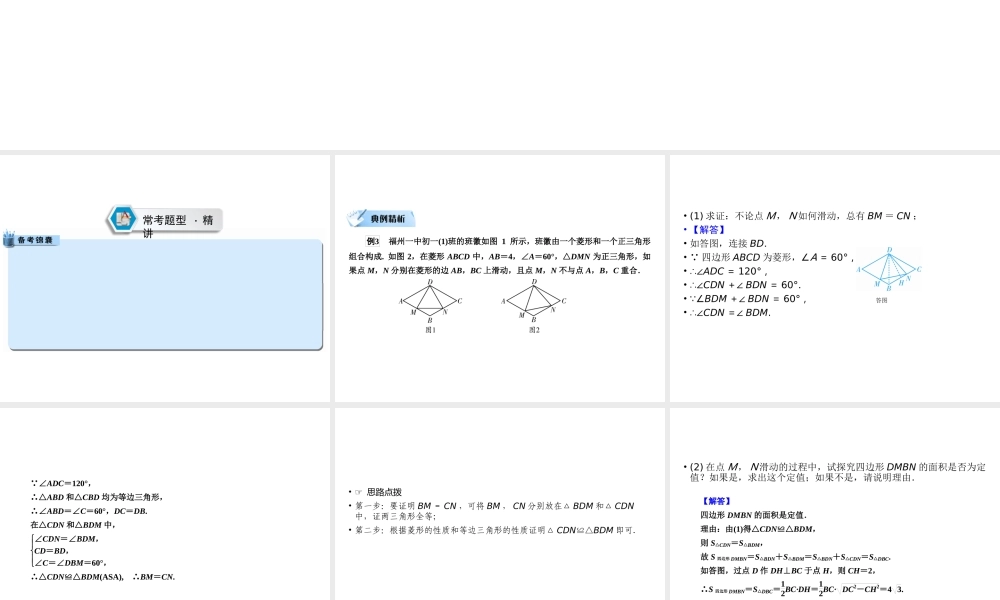
热点专题解读第二部分 专题八 动点型几何探究问题题型三 动点与最值问题• 动点与最值问题中的动点一般包括两种情况:即一点动和两点动;最值主要是线段最值 ( 包括周长 ) 和面积最值,线段主要是求最小值 . 当动点只有一个时,通过轴对称,将动点所在直线同侧的两个定点中的其中一个,映射到直线的另一侧,当动点在这个定点的对称点及另一定点的线段上时,由“两点之间线段最短”可知线段和有最小值,最小值为定点线段的长;当有两个动点时,并且两个动点的距离保持不变,用平移法可把两个动点变成一个动点来解决;确定面积最值时,常结合线段的最值来解决,或利用二次函数的性质来确定最值. 常考题型 · 精讲例3 福州一中初一(1)班的班徽如图 1 所示,班徽由一个菱形和一个正三角形组合构成. 如图 2,在菱形 ABCD 中,AB=4,∠A=60°,△DMN 为正三角形,如果点 M,N 分别在菱形的边 AB,BC 上滑动,且点 M,N 不与点 A,B,C 重合. • (1) 求证:不论点 M, N 如何滑动,总有 BM = CN ;• 【解答】• 如答图,连接 BD.• 四边形 ABCD 为菱形,∠A = 60° ,• ∴∠ADC = 120° ,• ∴∠CDN +∠ BDN = 60°.• ∠BDM +∠ BDN = 60° ,• ∴∠CDN =∠ BDM.答图 ∠ADC=120°, ∴△ABD 和△CBD 均为等边三角形, ∴∠ABD=∠C=60°,DC=DB. 在△CDN 和△BDM 中, ∠CDN=∠BDM,CD=BD,∠C=∠DBM=60°, ∴△CDN≌△BDM(ASA), ∴BM=CN. • ☞ 思路点拨• 第一步:要证明 BM = CN ,可将 BM , CN 分别放在△ BDM 和△ CDN中,证两三角形全等;• 第二步:根据菱形的性质和等边三角形的性质证明△ CDN≌△BDM 即可.• (2) 在点 M, N 滑动的过程中,试探究四边形 DMBN 的面积是否为定值?如果是,求出这个定值;如果不是,请说明理由.【解答】 四边形 DMBN 的面积是定值. 理由:由(1)得△CDN≌△BDM, 则 S△CDN=S△BDM, 故 S 四边形 DMBN=S△BDN+S△BDM=S△BDN+S△CDN=S△DBC. 如答图,过点 D 作 DH⊥BC 于点 H,则 CH=2, ∴S 四边形 DMBN=S△DBC=12BC·DH=12BC· DC2-CH2=4 3. • ☞ 思路点拨• 第一步:要求四边形 DMBN 的面积为定值,如果不能直接计算出面积,可通过面积转化法求解,观察可根据割补法求面积;• 第二步:由三角形全等得出 S...