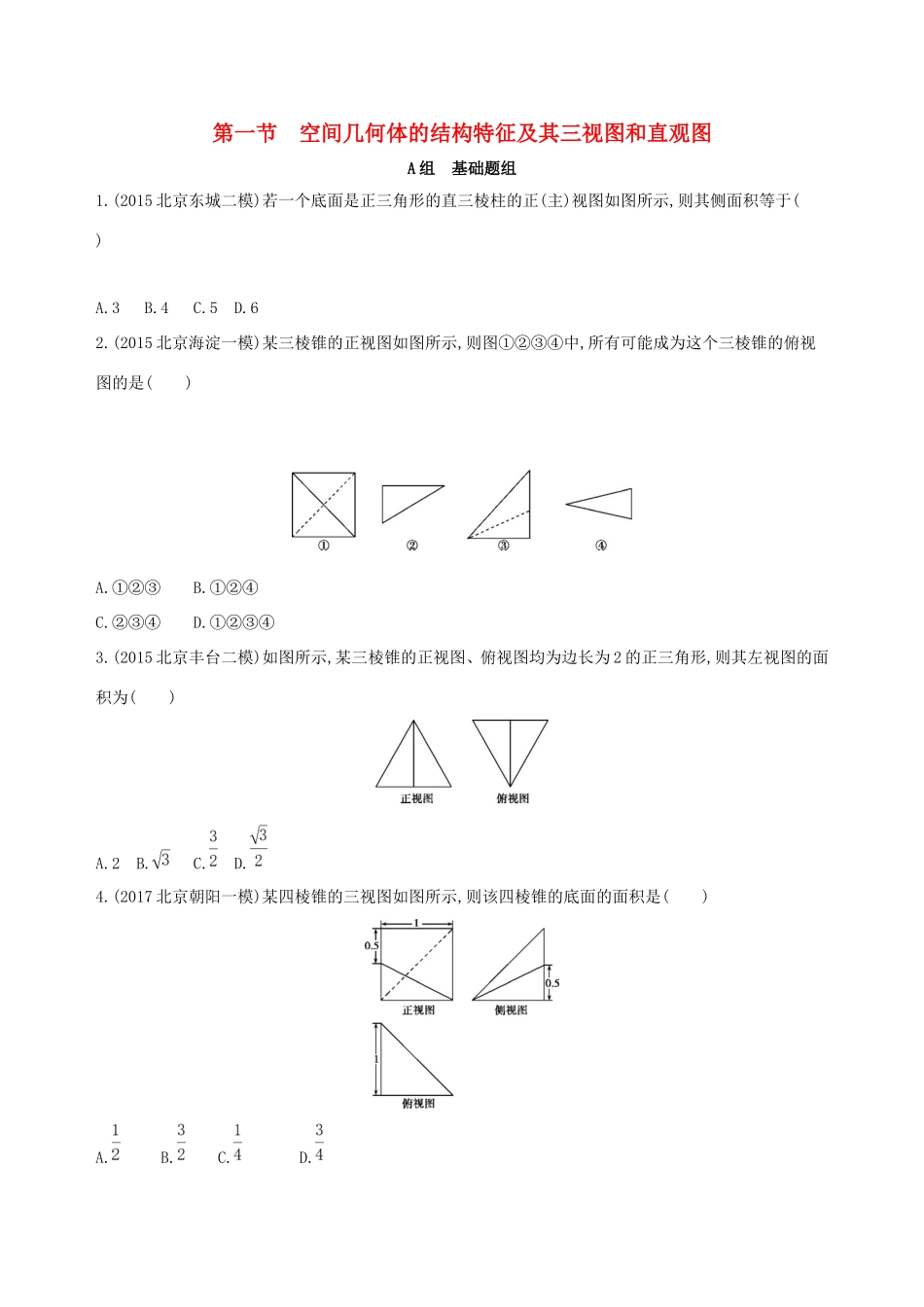
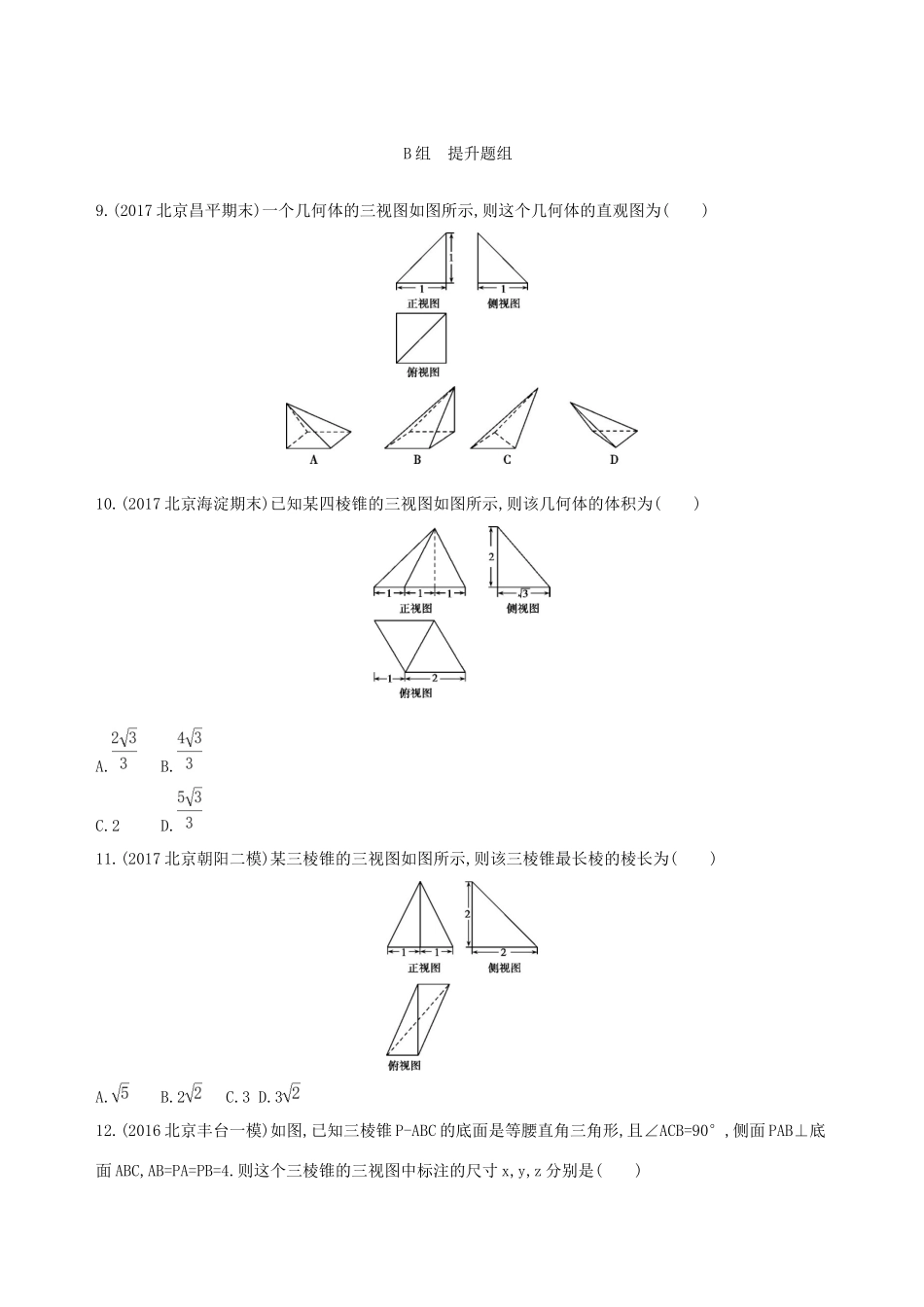
第一节空间几何体的结构特征及其三视图和直观图A组基础题组1.(2015北京东城二模)若一个底面是正三角形的直三棱柱的正(主)视图如图所示,则其侧面积等于()A.3B.4C.5D.62.(2015北京海淀一模)某三棱锥的正视图如图所示,则图①②③④中,所有可能成为这个三棱锥的俯视图的是()A.①②③B.①②④C.②③④D.①②③④3.(2015北京丰台二模)如图所示,某三棱锥的正视图、俯视图均为边长为2的正三角形,则其左视图的面积为()A.2B.C.D.4.(2017北京朝阳一模)某四棱锥的三视图如图所示,则该四棱锥的底面的面积是()A.B.C.D.5.(2016北京朝阳二模)已知某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长是()A.B.C.2D.6.(2017北京西城二模)某四面体的三视图如图所示,该四面体的体积为()A.B.2C.D.47.(2017北京西城模拟)某四棱锥的三视图如图所示,该四棱锥的表面积是()A.20+2B.14+4C.26D.12+28.(2015北京东城期末)某几何体的三视图如图所示(单位:cm),则该几何体最长棱的棱长为cm.B组提升题组9.(2017北京昌平期末)一个几何体的三视图如图所示,则这个几何体的直观图为()10.(2017北京海淀期末)已知某四棱锥的三视图如图所示,则该几何体的体积为()A.B.C.2D.11.(2017北京朝阳二模)某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为()A.B.2C.3D.312.(2016北京丰台一模)如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=90°,侧面PAB⊥底面ABC,AB=PA=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是()A.2,2,2B.4,2,2C.2,2,2D.2,2,213.(2018北京海淀期末)已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别是棱BC、C1D1的中点,点P在平面A1B1C1D1内,点Q在线段A1N上.若PM=,则PQ长度的最小值为()A.-1B.C.-1D.14.(2016北京西城二模)某四棱锥的三视图如图所示,则该四棱锥最长棱的长为.答案精解精析A组基础题组1.D由题意和三棱柱的正(主)视图可知该几何体为正三棱柱,其底面边长为2,高为1,故该三棱柱的侧面积S=3×2×1=6,故选D.2.D若俯视图为题图①,则其直观图可以为如图1所示的三棱锥A-BCD;若俯视图为题图②,则其直观图可以为如图2所示的三棱锥A-BCD;若俯视图为题图③,则其直观图可以为如图3所示的三棱锥A-BCD;若俯视图为题图④,则其直观图可以为如图4所示的三棱锥A-BCD.3.C由几何体的正视图和俯视图得该几何体的侧视图是底为,高为的直角三角形,则其面积为××=,故选C.4.D根据三视图将四棱锥还原到正方体中,如图中四棱锥P-ABCD,底面面积为=.故选D.5.A将几何体(三棱锥P-ABC)还原到长方体中,由三视图知该长方体的长、宽、高分别为2、1、1.如图所示.易得PA=1,AC=1,AB=,PB=,PC=,BC=.故该三棱锥最长棱的棱长是.6.A7.A8.答案解析由三视图可知该几何体为四棱锥,其直观图如图,其中PD⊥平面ABCD,ABCD为矩形,则易知PB是四棱锥最长的棱,易求得PB==cm.B组提升题组9.B由几何体的三视图可知,只有B项符合题意,故选B.10.B由三视图可知,几何体是以俯视图为底面,高为2的四棱锥,体积为×2××2=,故选B.11.C根据三视图,将三棱锥P-ABC还原到正方体中,如图.易知PA为最长棱,PB=2,AB=1,∴PA==3.12.C作PO⊥AB于O点,连接OC,则O为AB的中点,∵面PAB∩面ABC=AB,面PAB⊥面ABC,PO⊂面PAB,∴PO⊥面ABC.∴PO为几何体的高,在Rt△PAO中可求得PO=2,故x=2.∵在△ABC中,∠ACB=90°,AC=BC,∴由俯视图知2y=AB=4,z=OC=2.故x=2,y=2,z=2.13.C由题意知B1M=C1M=,取B1C1的中点M1,则P点轨迹是以M1为圆心,半径为1的半圆,建立以A1为原点,以A1B1,A1D1所在直线为x轴、y轴的平面直角坐标系,则B1(2,0),C1(2,2),M1(2,1),直线A1N的方程为y=2x,点M1到A1N的距离为,即PQ长度的最小值为-1,故选C.14.答案3解析由三视图将几何体(四棱锥P-ABCD)还原到棱长为2的正方体中,如图.∴PA=AB=AD=2,连接AC,易得PB=PD=2,CD=AC=,BC=1,∴PC===3,∴最长棱的棱长为3.