高中数学 平面向量的数量积及向量应用课后练习一 新人教A版必修4VIP免费

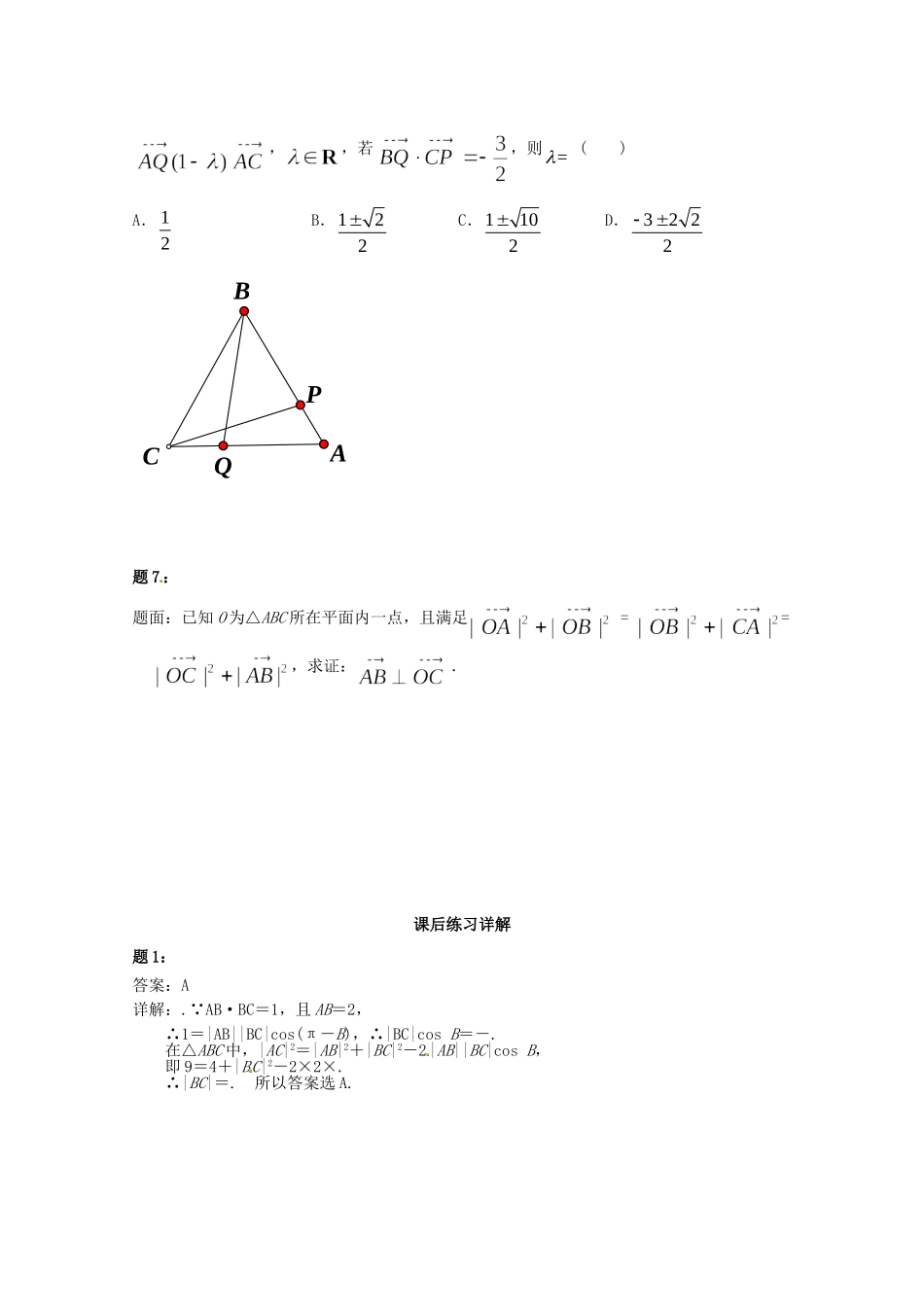
题1：题面：在△ABC中，AB＝2，AC＝3，AB·BC＝1，则BC＝()A.B.C．2D.题2：题面：已知平面上三点A、B、C满足||＝6，||＝8，||＝10，则的值等于()A．100B．96C．－100D．－96题3：题面：已知非零向量a，b满足|a＋b|＝|a－b|＝|a|，则a＋b与a－b的夹角为()A．30°B．60°C．120°D．150°题4：题面：已知点O，N，P在△ABC所在平面内，且|OA|＝|OB|＝|OC|，NA＋NB＋NC＝0，PA·PB＝PB·PC＝PC·PA，则点O、N、P依次是△ABC的()A．重心、外心、垂心B．重心、外心、内心C．外心、重心、垂心D．外心、重心、内心题5：题面：已知|a|＝|b|＝2，(a＋2b)·(a－b)＝－2，则a与b的夹角为________．题6：题面：已知△ABC为等边三角形，=2AB，设点P，Q满足，，，若，则=()A．12B．122C．1102D．3222CBAPQ题7：题面：已知O为△ABC所在平面内一点，且满足==，求证：．课后练习详解题1：答案：A详解：.∵AB·BC＝1，且AB＝2，∴1＝|AB||BC|cos(π－B)，∴|BC|cosB＝－.在△ABC中，|AC|2＝|AB|2＋|BC|2－2|AB||BC|cosB，即9＝4＋|BC|2－2×2×.∴|BC|＝.所以答案选A.题2：答案：C详解：∵||＝6，||＝8，||＝10，62＋82＝102.∴△ABC为Rt△.即＝0.答案：C题3：答案：B详解：将|a＋b|＝|a－b|两边同时平方得：a·b＝0；将|a－b|＝|a|两边同时平方得：b2＝a2.所以cos＝＝＝.所以＝60°.答案：B题4：答案：C详解：由|OA|＝|OB|＝|OC|知O到A、B、C三点的距离相等，即为外心．由NA＋NB＋NC＝0，设D为BC中点，则有NA＋2ND＝0.则N为中线靠近中点的三等分点，即为重心．由PA·PB＝PB·PC⇒PB·(PC－PA)＝0⇒PB·AC＝0，同理，有PA·BC＝0，PC·AB＝0.则P为垂心，故选C.题5：答案：详解：∵(a＋2b)·(a－b)＝|a|2－2|b|2＋a·b＝－2且|a|＝|b|＝2，∴a·b＝2，∴cos＝＝.而∈[0，π]，∴＝.答案：题6：答案：A详解：∵，，又∵，且，，，∴，，所以234+2(1)+4(1)=2，解得1=2.所以选A.题7：答案：见详解详解：设=a，=b，=c，则=cb，=ac，=ba由题设：==，化简：a2+(cb)2=b2+(ac)2=c2+(ba)2得：c•b=a•c=b•a从而•=(ba)•c=b•ca•c=0∴同理：，