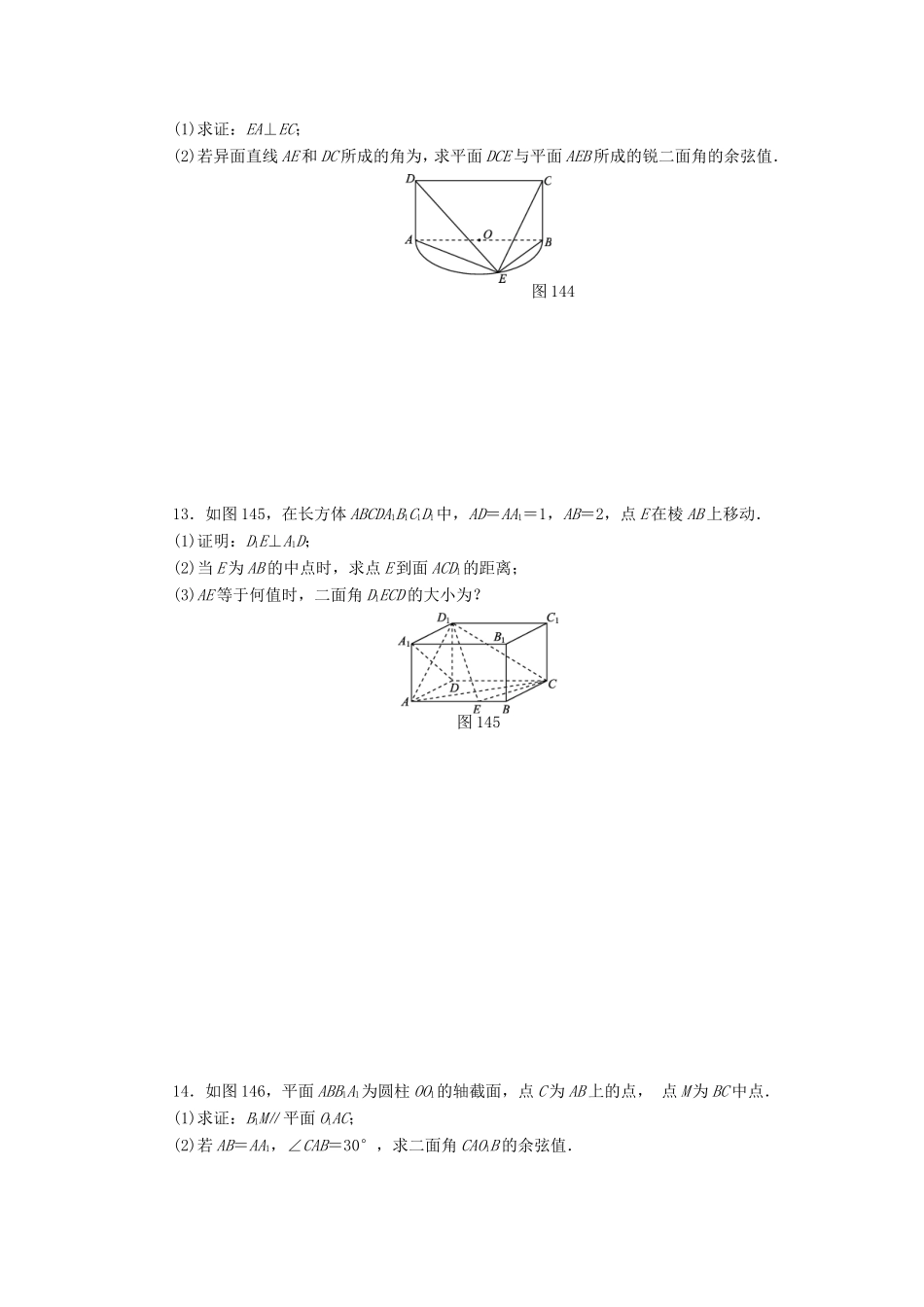
专题限时集训(十四)A[空间向量与立体几何](时间:10分钟+35分钟)基础演练夯知识1.直线l1的方向向量s1=(1,0,-2),直线l2的方向向量s2=(-1,2,2),则直线l1,l2所成角的余弦值是()A.B.-C.D.-2.平面α,β的法向量分别是n1=(1,1,1),n2=(-1,0,-1),则平面α,β所成锐二面角的余弦值是()A.B.-C.D.-3.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的单位法向量是()A.±(1,1,1)B.±C.±D.±4.已知a,b是两个非零的向量,α,β是两个平面,下列命题中正确的是()A.a∥b的必要条件是a,b是共面向量B.a,b是共面向量,则a∥bC.a∥α,b∥β,则α∥βD.a∥α,b∥β,则a,b不是共面向量5.若a⊥b,a⊥c,l=αb+βc(α,β∈R),m∥a,则m与l一定()A.共线B.相交C.垂直D.不共面提升训练强能力图1416.如图141所示,三棱锥ABCD的棱长全相等,E为AD的中点,则直线CE与BD所成角的余弦值为()A.B.C.D.7.在正方体ABCDA1B1C1D1中,E是C1D1的中点,则异面直线DE与AC所成角的余弦值为()A.B.C.-D.-8.对于空间任意一点O和不共线的三点A,B,C,有OP=xOA+yOB+zOC(x,y,z∈R),则x=2,y=-3,z=2是P,A,B,C四点共面的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分又不必要条件图1429.如图142,在长方体ABCDA1B1C1D1中,体对角线B1D与平面A1BC1相交于点E,则点E为△A1BC1的()A.垂心B.内心C.外心D.重心10.考虑向量m=(a,b,0),n=(c,d,1),其中a2+b2=c2+d2=1.如下说法中正确的有________.(写出所有正确说法的编号)①向量n与z轴正方向的夹角恒为定值(即与c,d值无关);②m·n的最大值为;③〈m,n〉(m,n的夹角)的最大值为;④ad-bc的值可能为;⑤若定义u×v=|u|·|v|sin〈u,v〉,则|m×n|的最大值为.11.如图143,在四棱锥P143ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,AB=2PA,E为BC的中点.(1)求证:AD⊥PE;(2)求平面APE与平面PCD所成锐二面角的余弦值.图14312.如图144所示,E是以AB为直径的半圆O上异于A,B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.(1)求证:EA⊥EC;(2)若异面直线AE和DC所成的角为,求平面DCE与平面AEB所成的锐二面角的余弦值.图14413.如图145,在长方体ABCDA1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;(2)当E为AB的中点时,求点E到面ACD1的距离;(3)AE等于何值时,二面角D1ECD的大小为?图14514.如图146,平面ABB1A1为圆柱OO1的轴截面,点C为AB上的点,点M为BC中点.(1)求证:B1M∥平面O1AC;(2)若AB=AA1,∠CAB=30°,求二面角CAO1B的余弦值.图146K专题限时集训(十四)B[空间向量与立体几何](时间:10分钟+35分钟)基础演练夯知识1.如图147所示,三棱锥PABC中,∠ACB=90°,PA⊥底面ABC.(1)求证:平面PAC⊥平面PBC;(2)若AC=BC=PA,M是PB的中点,求AM与平面PBC所成角的正切值.图1472.如图148所示,在四棱锥PABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.(1)求证:平面EFG∥平面PCD;(2)求二面角DEFB的平面角的大小.图148提升训练强能力3.如图149所示,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,使BD=3,得到三棱锥BACD.(1)若M是BC的中点,求证:在三棱锥BACD中,直线OM与平面ABD平行;(2)求二面角ABDO的余弦值;(3)设点N是BD上的一个动点,试确定N点的位置,使得CN=4.图1494.如图1410所示,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=CD=2,点M在EC上,且不与E,C重合.(1)当点M是EC的中点时,求证:BM∥平面ADEF;(2)当平面BDM与平面ABF所成的锐二面角的余弦值为时,求三棱锥MBDE的体积.图14105.如图1411所示,已知直角梯形ABCD中,AB∥CD,AD⊥AB,△CDE是边长为2的等边三角形,AB=5.沿CE将△BCE折起,使B至B′处,且B′C⊥DE,然后再将△ADE沿DE折起,使A至A′处,且平面A′DE⊥平面CDE.△B′CE和△A′DE在平面CDE的同侧.(1)求证:B′C⊥平面CDE;(2)求平面B′A′D与平面CDE所成的锐二面...