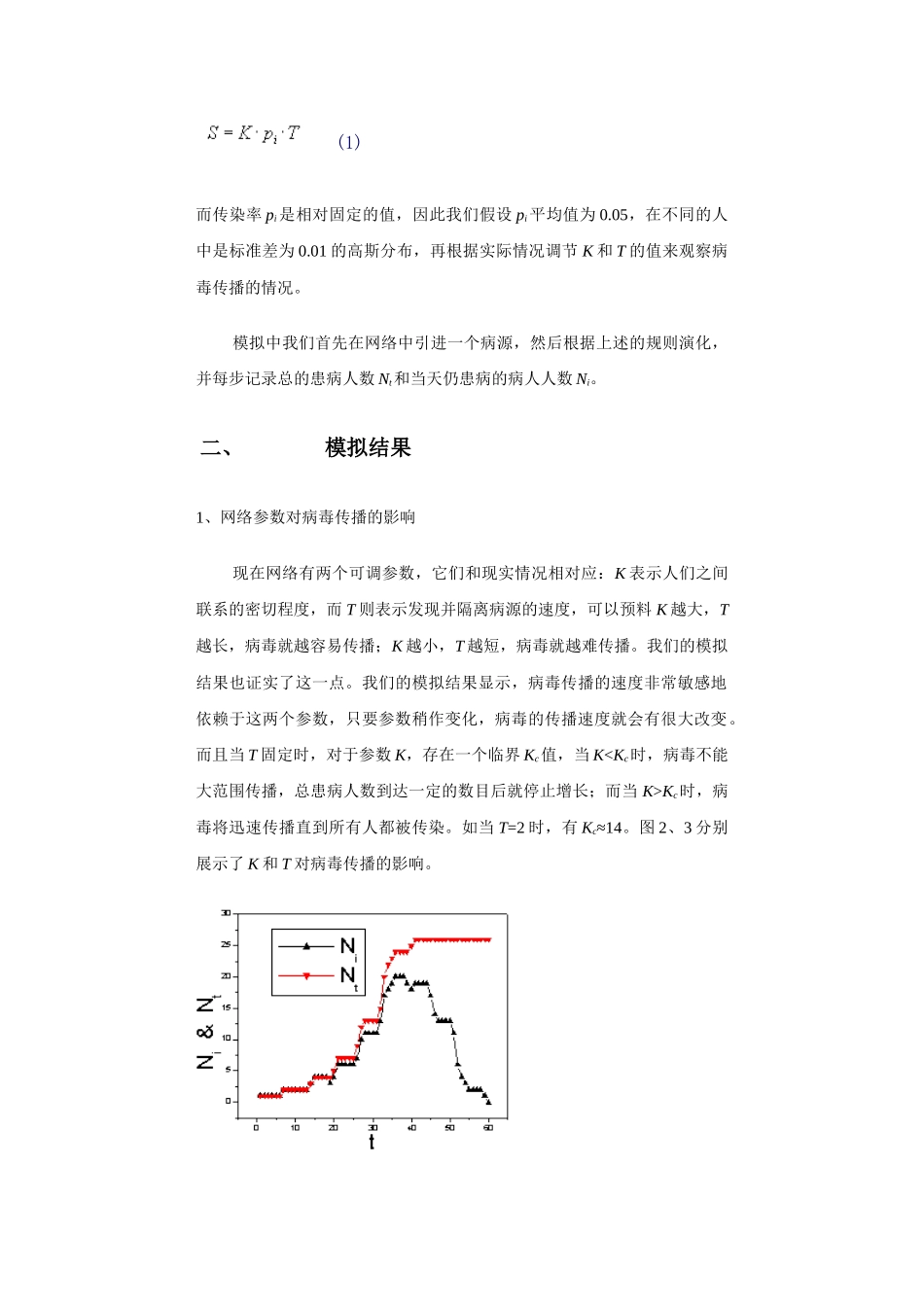
用小世界网络模型研究SARS病毒的传播林国基,贾珣,欧阳颀北京大学物理学院非线性实验室,北京大学理论生物中心本文用小世界网络模型模拟SARS病毒的传播,成功得到了和现实病毒扩散相同的趋势,同时指出与病毒传播速度相关的网络参量,并通过引入网络反馈提出控制病毒传播的几种可能的手段和以后的发展可能性。一、模型介绍流行病传播模型是时空动力学模型。传统理论的主要基本假设把社会中人与人的关系看成规则网络,主要的预测模型是反应——扩散模型。随着现代化交通工具的发展,此模型已经不能如实反映传染病传播的实际情况。近年来,大量的统计数据表明,社会网络模型应该是“小世界”模型。“小世界”概念是近年来复杂性科学研究的一个新成果,已经在许多应用领域得到应用。如互联网控制,爱滋病传播预测,生物学蛋白质网络动力学研究等。由现代交通工具带来的社会网络的新特点,研究现代流行病传播必须考虑小世界网络模型。小世界网络模型是Watts和Strogatz在1998年提出的基于人类社会网络的网络模型,它通过调节一个参数可以从规则网络向随机网络过渡。这个模型的构造算法是:从一个环状的规则网络开始,网络含有N个结点,每个结点向与它最近邻的K个结点连出K条边,并满足N>>K>>ln(N)>>1。对每一条边,有p的概率改变它的目的连接点来重新连接此边,并保证没有重复的边出现,这样就会产生pNK/2条长程的边把一个结点和远处的结点联系起来。改变p值可以实现从规则网络(p=0)向随机网络(p=1)转变。图1展示了小世界网络的构造过程:小世界网络模型的“小世界”主要特征之一是结点之间的平均距离随远程连接的个数而指数下降,对于规则网络,平均距离L可估计为;而对于小世界网络模型,,例如,对于一个千万人口的城市,人与人的平均接触距离时6左右。这使得社会人群之间的距离大大缩短。图1.小世界网络的构造过程以及从规则网络向随机网络的过渡。图中有N=20,K=4。我们把社会中的人们看成是网络的结点,把人们之间的亲密接触关系表示为结点间的连接边。在模拟中我们取网络的大小为N=1000000,p=0.01,K值作为一调节参量待定。根据SARS病毒的传播规律,我们把一个人的感染周期分为三个阶段:潜伏期、传染期和隔离期。一个人被感染后进入潜伏期,这个时期没有传染性,假设潜伏期平均为6天,在不同的人中是标准差为2天的高斯分布。然后病人进入天数为T的传染期,在此期间每天每个和他有亲密接触关系的人都有pi的概率被传染,接着病人被隔离治疗,隔离期我们假设为10天,最后病人康复重新进入网络中,忽略掉病人死亡的情况。在这里病毒传染情况可以用一个量S来表示:(1)而传染率pi是相对固定的值,因此我们假设pi平均值为0.05,在不同的人中是标准差为0.01的高斯分布,再根据实际情况调节K和T的值来观察病毒传播的情况。模拟中我们首先在网络中引进一个病源,然后根据上述的规则演化,并每步记录总的患病人数Nt和当天仍患病的病人人数Ni。二、模拟结果1、网络参数对病毒传播的影响现在网络有两个可调参数,它们和现实情况相对应:K表示人们之间联系的密切程度,而T则表示发现并隔离病源的速度,可以预料K越大,T越长,病毒就越容易传播;K越小,T越短,病毒就越难传播。我们的模拟结果也证实了这一点。我们的模拟结果显示,病毒传播的速度非常敏感地依赖于这两个参数,只要参数稍作变化,病毒的传播速度就会有很大改变。而且当T固定时,对于参数K,存在一个临界Kc值,当KKc时,病毒将迅速传播直到所有人都被传染。如当T=2时,有Kc≈14。图2、3分别展示了K和T对病毒传播的影响。图2.平均连接边数K对病毒传播的影响,两图均有T=2。左图K=10,病毒传播自动衰减;右图K=20,病毒迅速传播。图3.传染期时间T对病毒传播的影响。可以看到T只要增加1天,传染的速度就会大幅度增加,其中K=20。由图3可见,不能及时发现病源和人们之间接触太多会非常有利于病毒的传播,初期出现病毒的爆发正是由于这两个原因,要控制病毒的蔓延也正是要从这两个方面入手。2、引入反馈机制后对病毒传播的影响如果不引入其它的机制,那么...