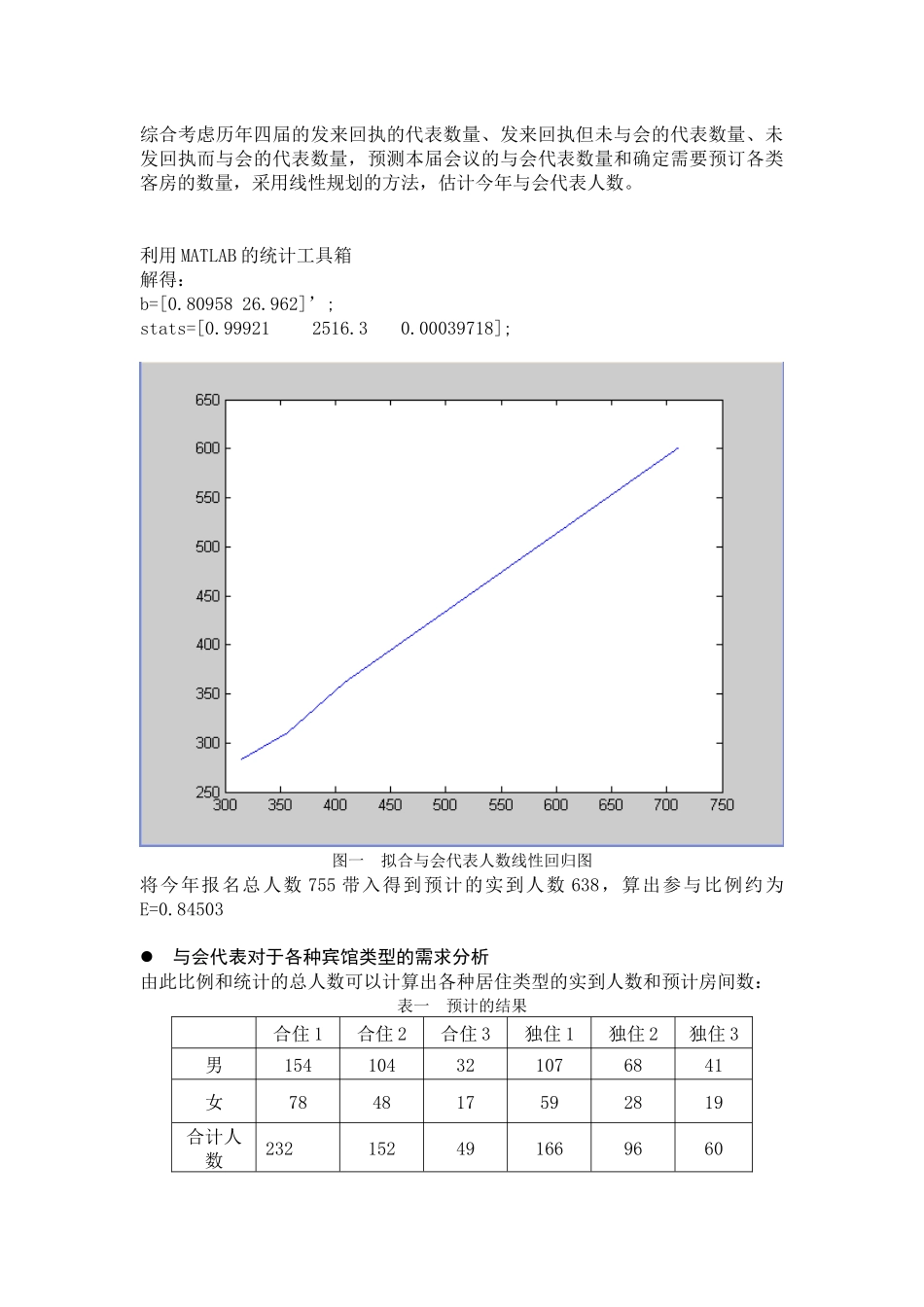
...../更多资料请访问.(.....)...../会议筹备问题摘要为了确定最合适的宾馆以及房间和会议室的预定,综合考虑与会代表满意度、会议成本、组织的方便程度等多方面的因素,从经济,方便等方面对所给的会议筹备问题进行了全面的优化设计。建立以下三个模型:模型一:通过线性规划的方法,考虑历年四届的发来回执的代表数量、发来回执但未与会的代表数量、未发回执而与会的代表数量,预测本届会议的与会代表数量和确定需要预订各类客房的数量。模型二:在模型一的基础上,为了便于管理,以宾馆总数最少为目标,以满足代表在合住、独住及价位方面的需求,及各宾馆拥有客房数量等为约束条件,通过整数规划建立优化模型,确定选择的宾馆以及预定的各宾馆的房间数。模型三:在模型二的基础上,确定会议室和租车方案。利用题意合理简化,使模型便于讨论,再排除明显的非最优解,对余下情况一一讨论,得到合理方案。问题的提出会议筹备中经常遇到以下问题:通常与会代表多达数百人,而适于接待的宾馆数有限,只能让代表分散到多家宾馆。然而有些发来回执的代表不来参加会议,而有些来参加会议的代表实现不发来回执。虽然客房费用由代表自理,但如果预定的数量大于实际数量,筹备组需支付一天的空房费用,引起不必要的损失,而若预定的客房数量不足,则将引起代表的不满带来负面效应。而且内容不同的分组会分散到几个宾馆,而代表要参加哪个分组会无法预知,因此需要派车在宾馆间接送。本次建模过程中主要解决以下问题:问题1:预测本届会议代表的数量,并确定预定各类客房的数量。问题2:确定在哪些宾馆预定客房以及预定各类客房的数量。问题3:确定在哪些宾馆预定哪些类型的会议室以及租车的规格和数量。分析与假设在题意的基础上,假设以下条件成立:每个会议代表之间是独立的;宾馆内的每个房间是可预订的;每个与会代表参加会议概率是相等的,每个代表都参加两次会议,分别是上下午各一场每辆车只能单向接送,不可往返接送目的地在200米距离以内无需租车上午参加完会议代表回到自己住宿地点,保证下午情况与上午完全相同假定每位来宾参加六个会议的几率相等。变量说明:需要预订合住第j种类型客房数量T1j需要预订独住第j种类型客房数量T2j第i家宾馆第j种类型双人房(合住或独住)能提供的间数C1ij第i家宾馆第j种类型双人房(独住)能提供的间数C2ij设共有r家宾馆双人,单人房各s(=3)种类型预订第i家宾馆第j种类型双人房(合住)间数x1ij预订第i家宾馆第j种类型单人房(独住)间数x2ij预订第i家宾馆第j种类型双人房(改独住)间数yij第i家宾馆的选择变量ki(ki=0,1)设ki=¿{0如果该宾馆未被选中¿¿¿¿基本模型的建立与求解模型一:与会代表人数的估计综合考虑历年四届的发来回执的代表数量、发来回执但未与会的代表数量、未发回执而与会的代表数量,预测本届会议的与会代表数量和确定需要预订各类客房的数量,采用线性规划的方法,估计今年与会代表人数。利用MATLAB的统计工具箱解得:b=[0.8095826.962]’;stats=[0.999212516.30.00039718];图一拟合与会代表人数线性回归图将今年报名总人数755带入得到预计的实到人数638,算出参与比例约为E=0.84503与会代表对于各种宾馆类型的需求分析由此比例和统计的总人数可以计算出各种居住类型的实到人数和预计房间数:表一预计的结果合住1合住2合住3独住1独住2独住3男154104321076841女784817592819合计人数232152491669660按比例实到人数196.05128.4441.406140.2781.12350.702预计房间数9965211418251注:预计双人间房间数为按比例实际到达人数除以2向上取整,单间直接向上取整模型二:在模型一的基础上,为了便于管理,以宾馆总数最少为目标,以满足代表在合住、独住及价位方面的需求,及各宾馆拥有客房数量等为约束条件,通过整数规划建立优化模型,确定选择的宾馆以及预定的各宾馆的房间数。各宾馆对于各类型的房间供应分析由题意可得下表:表二各个宾馆提供的相应住房数双人房单人房120~160161~200201~300120~160161~200201~300①0503003020②85750000③502402700④50450000⑤70400000⑥0403040300⑦500040030⑧404000...