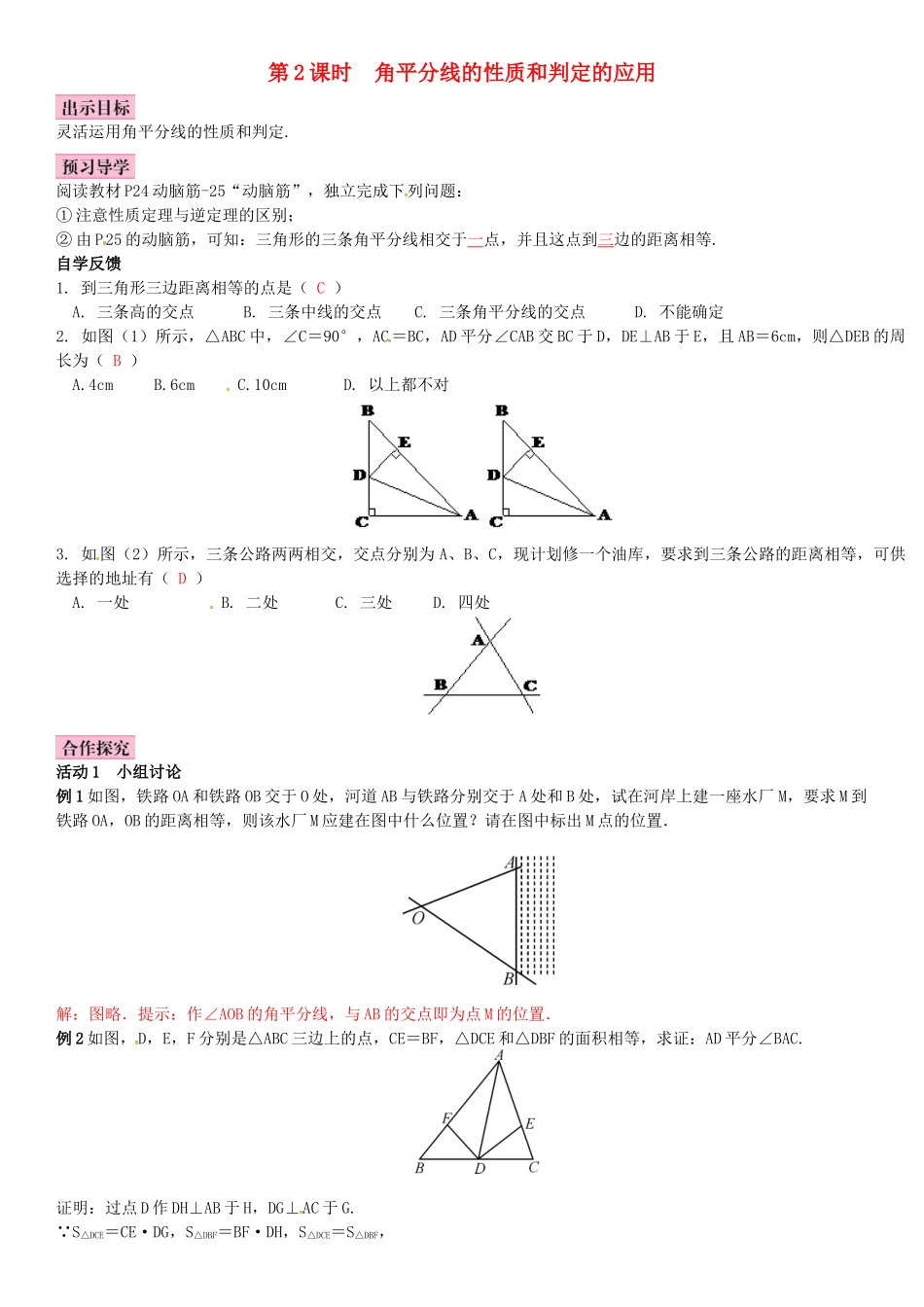
第2课时角平分线的性质和判定的应用灵活运用角平分线的性质和判定.阅读教材P24动脑筋-25“动脑筋”,独立完成下列问题:①注意性质定理与逆定理的区别;②由P25的动脑筋,可知:三角形的三条角平分线相交于一点,并且这点到三边的距离相等.自学反馈1.到三角形三边距离相等的点是(C)A.三条高的交点B.三条中线的交点C.三条角平分线的交点D.不能确定2.如图(1)所示,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为(B)A.4cmB.6cmC.10cmD.以上都不对3.如图(2)所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有(D)A.一处B.二处C.三处D.四处活动1小组讨论例1如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.解:图略.提示:作∠AOB的角平分线,与AB的交点即为点M的位置.例2如图,D,E,F分别是△ABC三边上的点,CE=BF,△DCE和△DBF的面积相等,求证:AD平分∠BAC.证明:过点D作DH⊥AB于H,DG⊥AC于G.∵S△DCE=CE·DG,S△DBF=BF·DH,S△DCE=S△DBF,∴CE·DG=BF·DH.又∵CE=BF,∴DG=DH.∴点D在∠BAC的平分线上,即AD平分∠BAC.例3如图:△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠BAF=180°.(1)求证:DE=DF;(2)若把最后一个条件改为:AE>AF,且∠AED+∠AFD=180°,那么结论还成立吗?解:(1)证明:过D作DM⊥AB,于M,DN⊥AC于N,即∠EMD=∠FND=90°,∵AD平分∠BAC,DM⊥AB,DN⊥AC,∴DM=DN(角平分线性质),∠DME=∠DNF=90°,∵∠EAF+∠EDF=180°,∴∠MED+∠AFD=360°-180°=180°,∵∠AFD+∠NFD=180°,∴∠MED=∠NFD,在△EMD和△FND中,,∴△EMD≌△FND(AAS),∴DE=DF.(2)成立.活动2跟踪训练1.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(C)A.10B.7C.5D.42.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是(A)A.M点B.N点C.P点D.Q点3.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为4.4.如图所示,在△ABC中,外角∠CBD、∠BCE的平分线交于O点,OF⊥AD,OG⊥AE,垂足分别为F、G,则OF=OG.(填“>”“<”或“=”)5.教材P25练习1、2活动3课堂小结