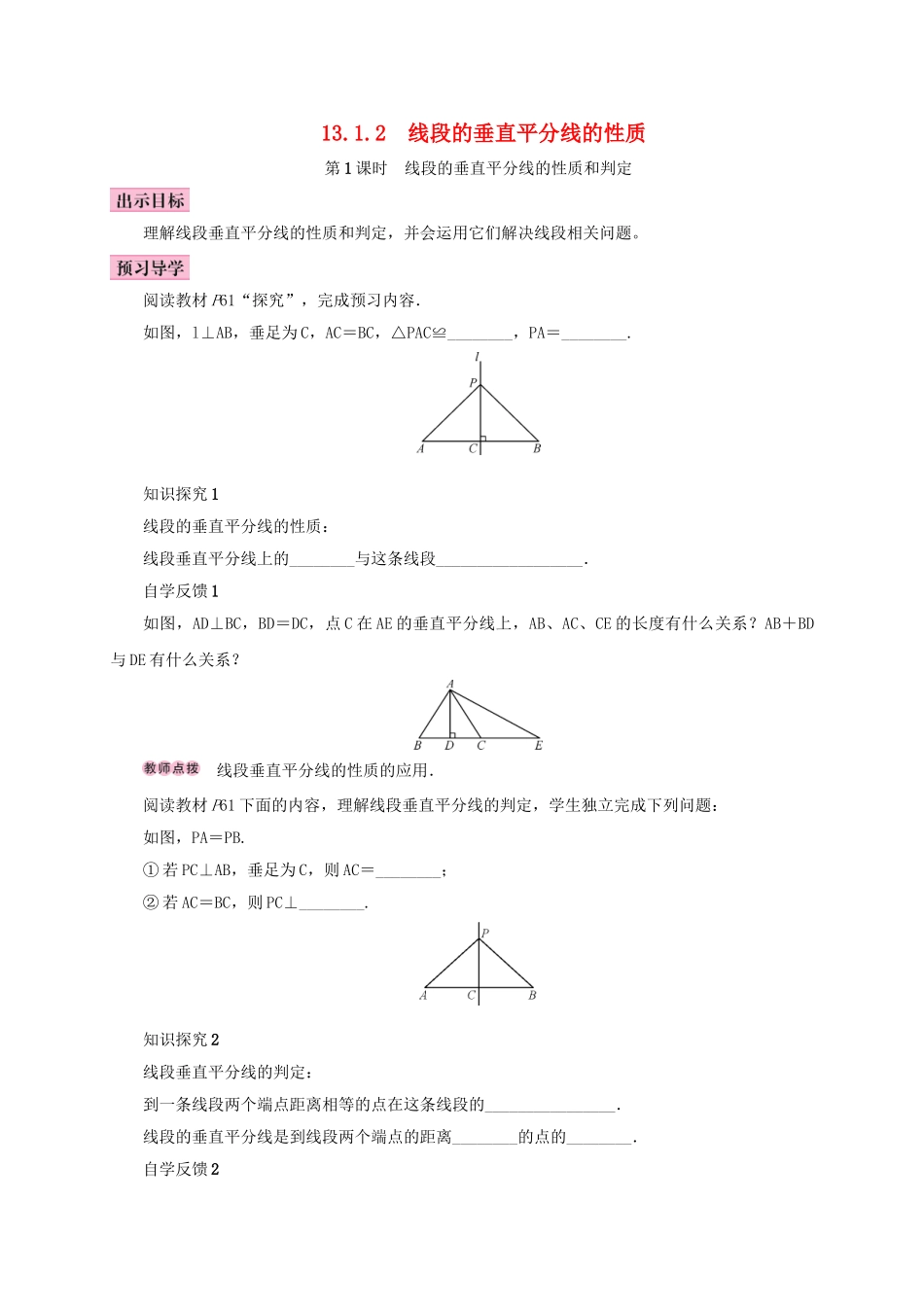
13.1.2线段的垂直平分线的性质第1课时线段的垂直平分线的性质和判定理解线段垂直平分线的性质和判定,并会运用它们解决线段相关问题。阅读教材P61“探究”,完成预习内容.如图,l⊥AB,垂足为C,AC=BC,△PAC≌________,PA=________.知识探究1线段的垂直平分线的性质:线段垂直平分线上的________与这条线段__________________.自学反馈1如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?线段垂直平分线的性质的应用.阅读教材P61下面的内容,理解线段垂直平分线的判定,学生独立完成下列问题:如图,PA=PB.①若PC⊥AB,垂足为C,则AC=________;②若AC=BC,则PC⊥________.知识探究2线段垂直平分线的判定:到一条线段两个端点距离相等的点在这条线段的________________.线段的垂直平分线是到线段两个端点的距离________的点的________.自学反馈21.下列条件中,不能判定直线MN是线段AB的垂直平分线的是()A.MA=MB,NA=NBB.MA=MB,MN⊥ABC.MA=NA,MB=NBD.MA=MB,MN平分∠AMB2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?可根据线段垂直平分线的判定证两个点都在BC的垂直平分线上,再根据两点确定一条直线得到直线AM是线段BC的垂直平分线.活动1小组讨论例1如图,AB=AC=8cm,AB的垂直平分线交AC于D,若△ADB的周长为18,求DC的长.解:∵DM是AB的垂直平分线,∴AD=BD.设CD的长为x,则AD=AC-CD=8-x.∵C△ADB=AB+AD+BD=8+(8-x)+(8-x)=18,∴x=3,即CD的长为3cm.由线段垂直平分线的性质得AD=BD进而求解.例2如图,△ABC中AC⊥DC,AD平分∠BAC,DE⊥AB于E,求证:直线AD是CE的垂直平分线.证明:∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴DE=CD.∴点D在CE的垂直平分线上.在Rt△AED与Rt△ACD中,∵AD=AD,DE=DC,∴Rt△AED≌Rt△ACD.∴AE=AC.∴点A在CE的垂直平分线上.∴直线AD是CE的垂直平分线.证线段垂直平分线的方法1即定义,证垂直平分,方法2即线段垂直平分线的判定方法.活动2跟踪训练1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为()A.6B.5C.4D.32.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC()A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点3.到平面内不在同一直线上的三个点A、B、C的距离相等的点有________个.4.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=________.5.如图,直线AD是线段BC的垂直平分线.求证:∠ABD=∠ACD.活动3课堂小结线段的垂直平分线的性质和判定有时是交叉使用的.【预习导学】△PBCPB知识探究1点两个端点的距离相等自学反馈1AB=AC=CE,AB+BD=DE.BCAB知识探究2垂直平分线上相等集合自学反馈21.C2.是.【合作探究】活动2跟踪训练1.B2.D3.14.155.证明:∵AD是BC的垂直平分线,∴AB=AC,BD=DC.∵AD=AD,∴△ABD≌△ACD.∴∠ABD=∠ACD.