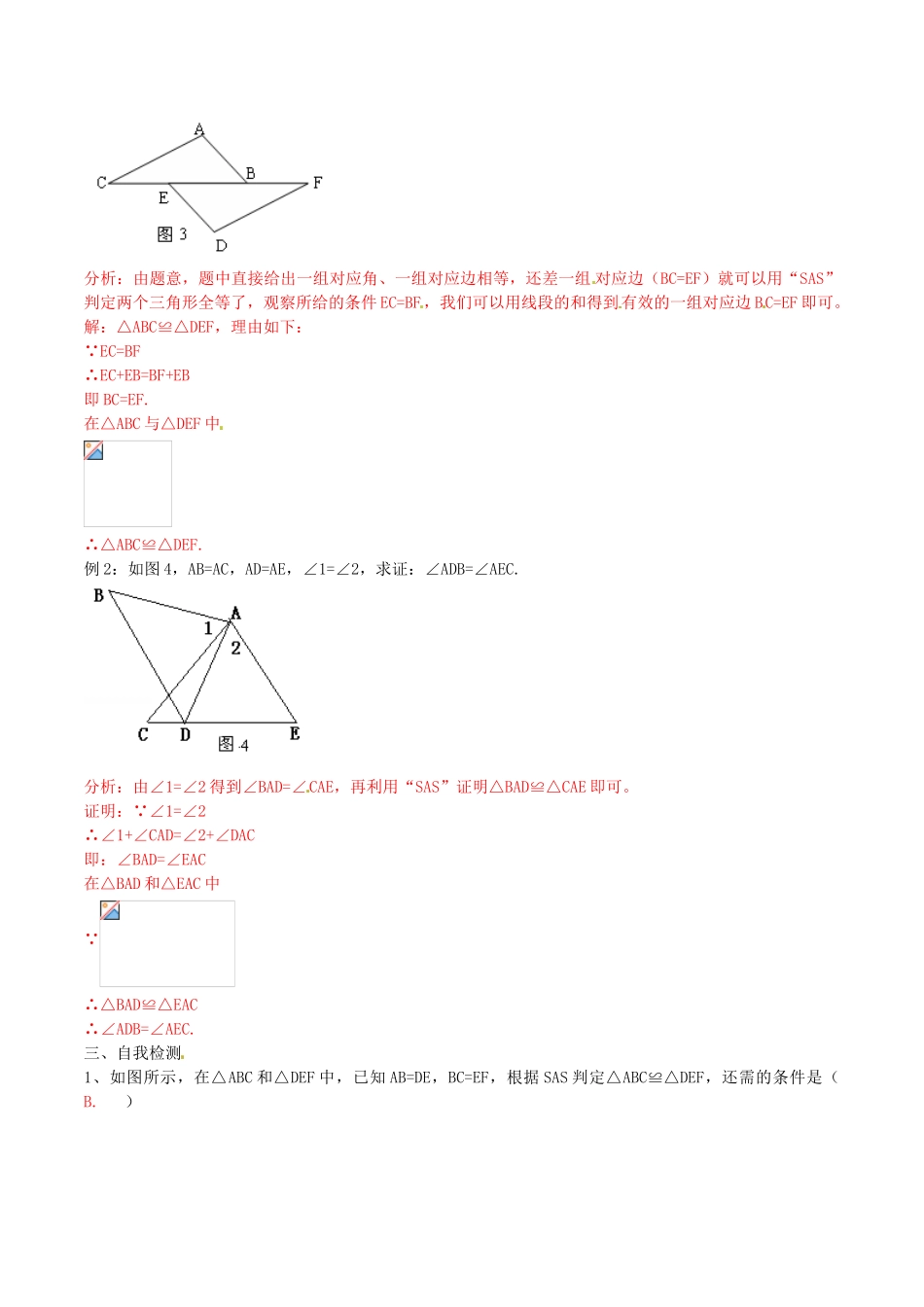
全等三角形的判定【学习目标】1.掌握SAS的内容,会运用SAS来识别两个三角形全等;2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学规律的过程;3、通过画图、思考、探究来激发学习的积极性和主动性。【学习重点】应用“边角边”证明两个三角形全等,进而得出线段或角相等.【学习难点】指导学生分析问题,寻找判定三角形全等的条件.一、学前准备如图1所示,AC、BD相交于O,AO、BO、CO、DO的长度如图所标,△ABO和△CDO是否能完全重合呢?不难看出,这两个三角形有三对元素是相等的:(1)___OA___=___OC____(2)_____OB____=____OD_____(3)__∠AOB_____=__∠COD____如果把△ABO绕着点O顺时针方向旋转,因为OA=OC,所以可以使OA与__OC___重合;又因为∠AOB=_∠COD_,OB=___OD___,所以点B与点__D___重合。这样△ABO与___△CDO___就完全重合了。归纳:如果两个三角形有两边和它们的夹角对应相等,那么这两个三角形全等。二、探索思考[1、阅读P37探究3,(1)读句画图:①画∠DAE=30°,②在AD、AE上分别取B、C,使AB=4cm,AC=6cm.③连结BC,得△ABC.2、由上面探究便得到判定两个三角形全等的第二种方法:两边和它们的夹角___对应相等___的两个三角形全等(可以简写成“__边角边______”或“___SAS____”)。证明如下:如图2所示,在△ABC与△A′B′C′中,∴△ABC__≌___△A′B′C′(___SAS__)。例题探讨例1:如图3,点C、E、B、F在同一直线上,∠C=∠F,AC=DF,EC=BF,△ABC与△DEF全等吗?说明你的结论。分析:由题意,题中直接给出一组对应角、一组对应边相等,还差一组对应边(BC=EF)就可以用“SAS”判定两个三角形全等了,观察所给的条件EC=BF,我们可以用线段的和得到有效的一组对应边BC=EF即可。解:△ABC≌△DEF,理由如下:∵EC=BF∴EC+EB=BF+EB即BC=EF.在△ABC与△DEF中∴△ABC≌△DEF.例2:如图4,AB=AC,AD=AE,∠1=∠2,求证:∠ADB=∠AEC.分析:由∠1=∠2得到∠BAD=∠CAE,再利用“SAS”证明△BAD≌△CAE即可。证明:∵∠1=∠2∴∠1+∠CAD=∠2+∠DAC即:∠BAD=∠EAC在△BAD和△EAC中∵∴△BAD≌△EAC∴∠ADB=∠AEC.三、自我检测1、如图所示,在△ABC和△DEF中,已知AB=DE,BC=EF,根据SAS判定△ABC≌△DEF,还需的条件是(B.)A、∠A=∠DB、∠B=∠EC、∠C=∠FD、以上三个均可以2、如图所示,已知AD∥BC,AD=CB,求证:△ABD≌△CDB。证明:∵AD∥BC,∴∠ADB=∠CBD在△ABD和△CDB中∵∴△ABD≌△CDB.3、如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF。证明:在△ADC和△ABC中∵∴△ADC≌△ABC∴∠D=∠B又E、F分别是DC、BC的中点,∴DE=DC,BF=BC∴DE=BF在△ADE和△ABF中∴△ADE≌△ABF∴AE=AF四、课堂小结通过本节课学习,你有什么收获?