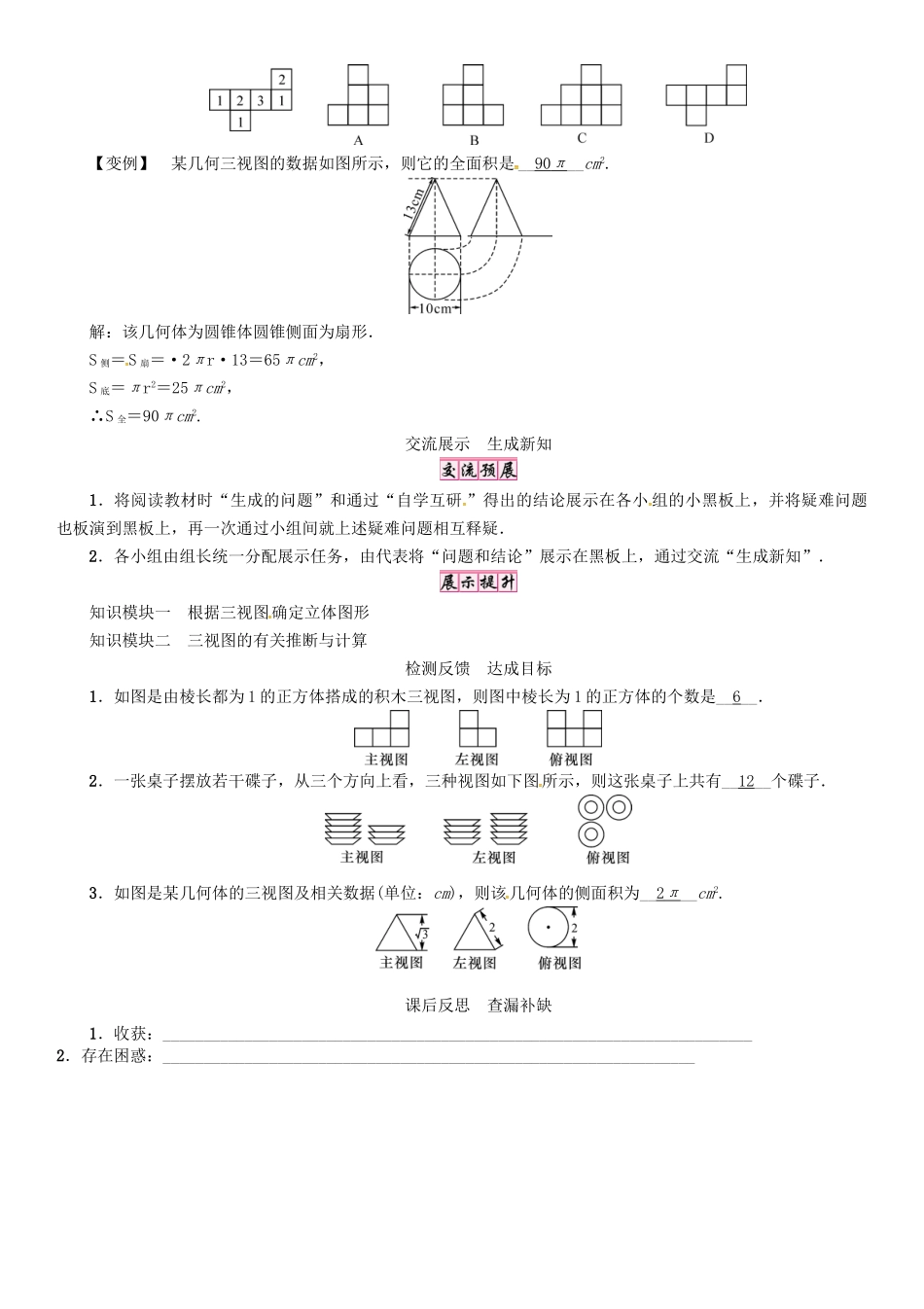
课题:已知三视图还原几何体【学习目标】1.进一步明确三视图意义,由三视图得出实物原型进行简单计算.2.让学生从三视图得出实物,培养学生的空间想象力.【学习重点】由三视图想象出实物原型.【学习难点】由三视图抽象出原型,进一步明确三视图的意义.情景导入生成问题旧知回顾:1.什么是物体的主视图?俯视图?左视图?答:从正面看到的图形称为该物体的主视图,从左面看到的图形称为该物体的左视图,从上面看到的图形称为该物体的俯视图.2.如图,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下列几何体中的哪一个?选择并说明理由.,A),B),C),D)答:要达到无缝隙地通过,B无方形视图,C,D无圆形视图,很显然是A.自学互研生成能力阅读教材P109~P110,完成下列问题:如何根据三视图想象立体图形?答:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.【例1】某几何体的三视图如图所示,则这个几何体是(D)A.圆柱B.正方体C.球D.圆锥【变例1】(永州中考)若某几何体的三视图如图所示,则这个几何体是(C)【变例2】一个几何体的三视图完全相同,该几何体可以是(D)A.圆锥B.圆柱C.长方体D.球【例2】(东营中考)下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置处小正方体的个数,则这个几何体的左视图是(B)【变例】某几何三视图的数据如图所示,则它的全面积是__90π__cm2.解:该几何体为圆锥体圆锥侧面为扇形.S侧=S扇=·2πr·13=65πcm2,S底=πr2=25πcm2,∴S全=90πcm2.交流展示生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的结论展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一根据三视图确定立体图形知识模块二三视图的有关推断与计算检测反馈达成目标1.如图是由棱长都为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是__6__.2.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有__12__个碟子.3.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为__2π__cm2.课后反思查漏补缺1.收获:________________________________________________________________________2.存在困惑:_________________________________________________________________