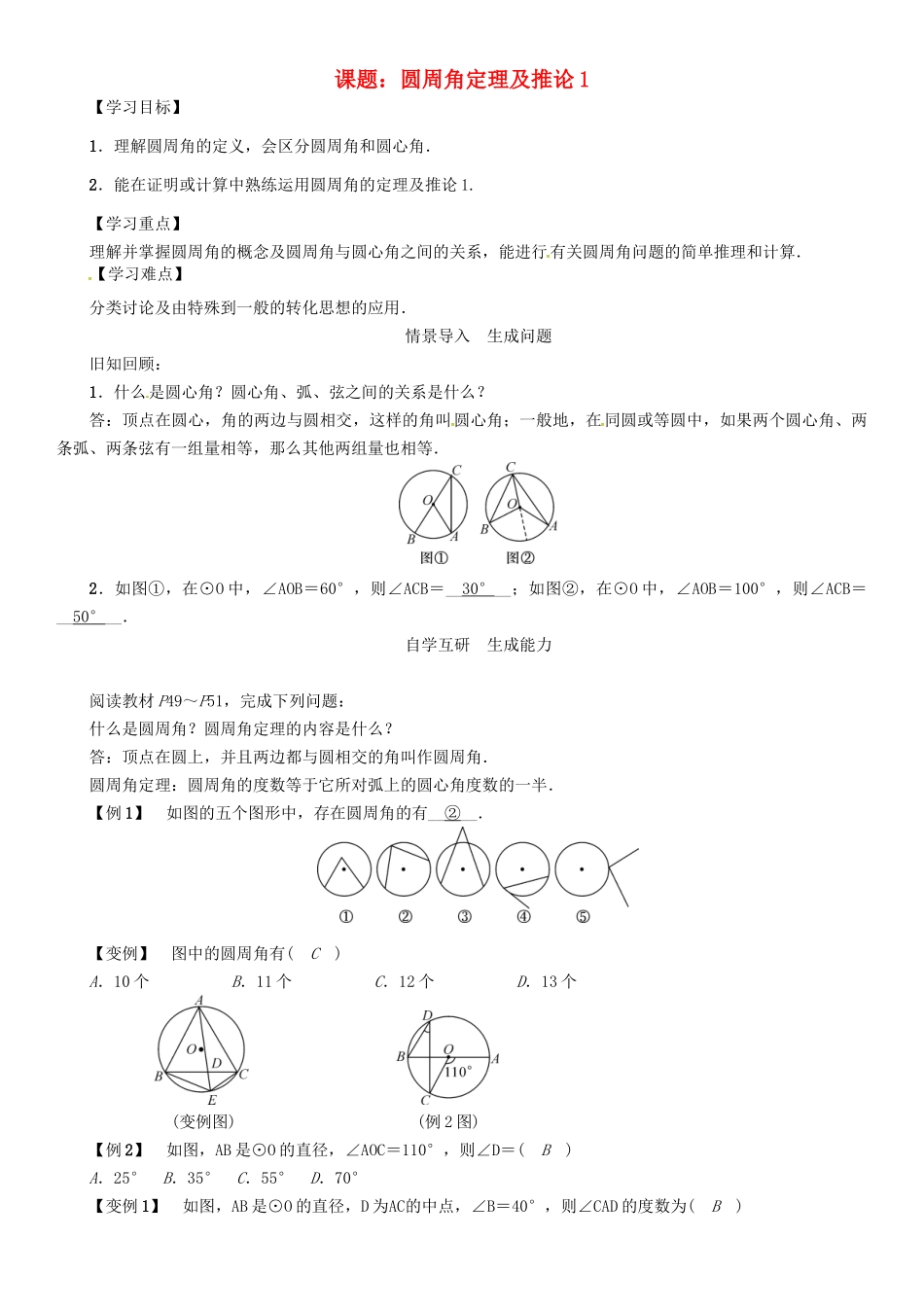
课题:圆周角定理及推论1【学习目标】1.理解圆周角的定义,会区分圆周角和圆心角.2.能在证明或计算中熟练运用圆周角的定理及推论1.【学习重点】理解并掌握圆周角的概念及圆周角与圆心角之间的关系,能进行有关圆周角问题的简单推理和计算.【学习难点】分类讨论及由特殊到一般的转化思想的应用.情景导入生成问题旧知回顾:1.什么是圆心角?圆心角、弧、弦之间的关系是什么?答:顶点在圆心,角的两边与圆相交,这样的角叫圆心角;一般地,在同圆或等圆中,如果两个圆心角、两条弧、两条弦有一组量相等,那么其他两组量也相等.2.如图①,在⊙O中,∠AOB=60°,则∠ACB=__30°__;如图②,在⊙O中,∠AOB=100°,则∠ACB=__50°__.自学互研生成能力阅读教材P49~P51,完成下列问题:什么是圆周角?圆周角定理的内容是什么?答:顶点在圆上,并且两边都与圆相交的角叫作圆周角.圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.【例1】如图的五个图形中,存在圆周角的有__②__.【变例】图中的圆周角有(C)A.10个B.11个C.12个D.13个(变例图)(例2图)【例2】如图,AB是⊙O的直径,∠AOC=110°,则∠D=(B)A.25°B.35°C.55°D.70°【变例1】如图,AB是⊙O的直径,D为AC的中点,∠B=40°,则∠CAD的度数为(B)A.10°B.20°C.30°D.40°,(变例1图)),(变例2图))【变例2】如图,AB,CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P=__40°__.圆周角定理的推论是什么?答:在同圆(或等圆)中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.【例3】如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=50°,点D是⊙O上一点,则∠D=(B)A.50°B.40°C.30°D.20°【变例1】(永州中考)如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知AB和CD所对的圆心角分别为90°和50°,则∠P=(D)A.45°B.40°C.25°D.20°,(例3图)),(变例1图)),(变例3图))【变例2】已知某个圆的弦长等于它的半径,则这条弦所对的圆周角的度数为__30°或150°__.【变例3】(黔西南中考)如图所示,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为__50°__.交流展示生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的结论展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一圆周角的概念及圆周角定理知识模块二圆周角定理的推论检测反馈达成目标1.(南昌中考)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为__110°__.2.如图,已知CD平分∠ACB,DE∥AC,求证:DE=BC.证明:∵CD平分∠ACB,∴∠ACD=∠BCD,∴BD=AD∵DE∥AC,∴∠ACD=∠CDE,∴CE=AD∴CE=BD∴BC=DE∴DE=BC.3.如图,已知△ABC内接于⊙O,E是BC的中点,AE交BC于点D.求证:BE2=AE·DE.证明:∵E是BC中点,∴BE=EC.∴∠BAE=∠EBD,又∵∠BED公用,∴△EDB∽△EBA.∴=.即BE2=AE·DE.课后反思查漏补缺1.收获:__________________________________________________________________2.存在困惑:___________________________________________________________________