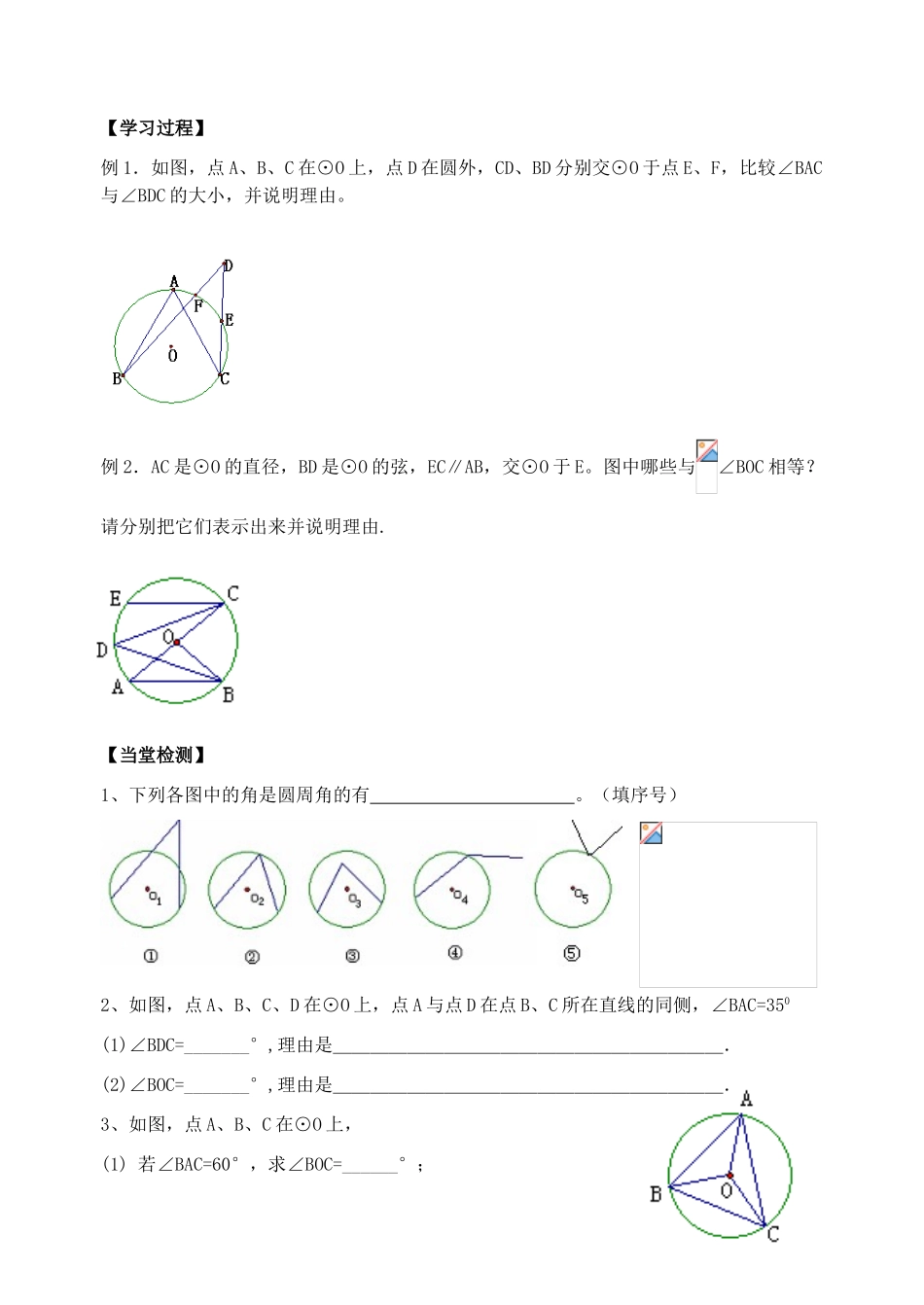
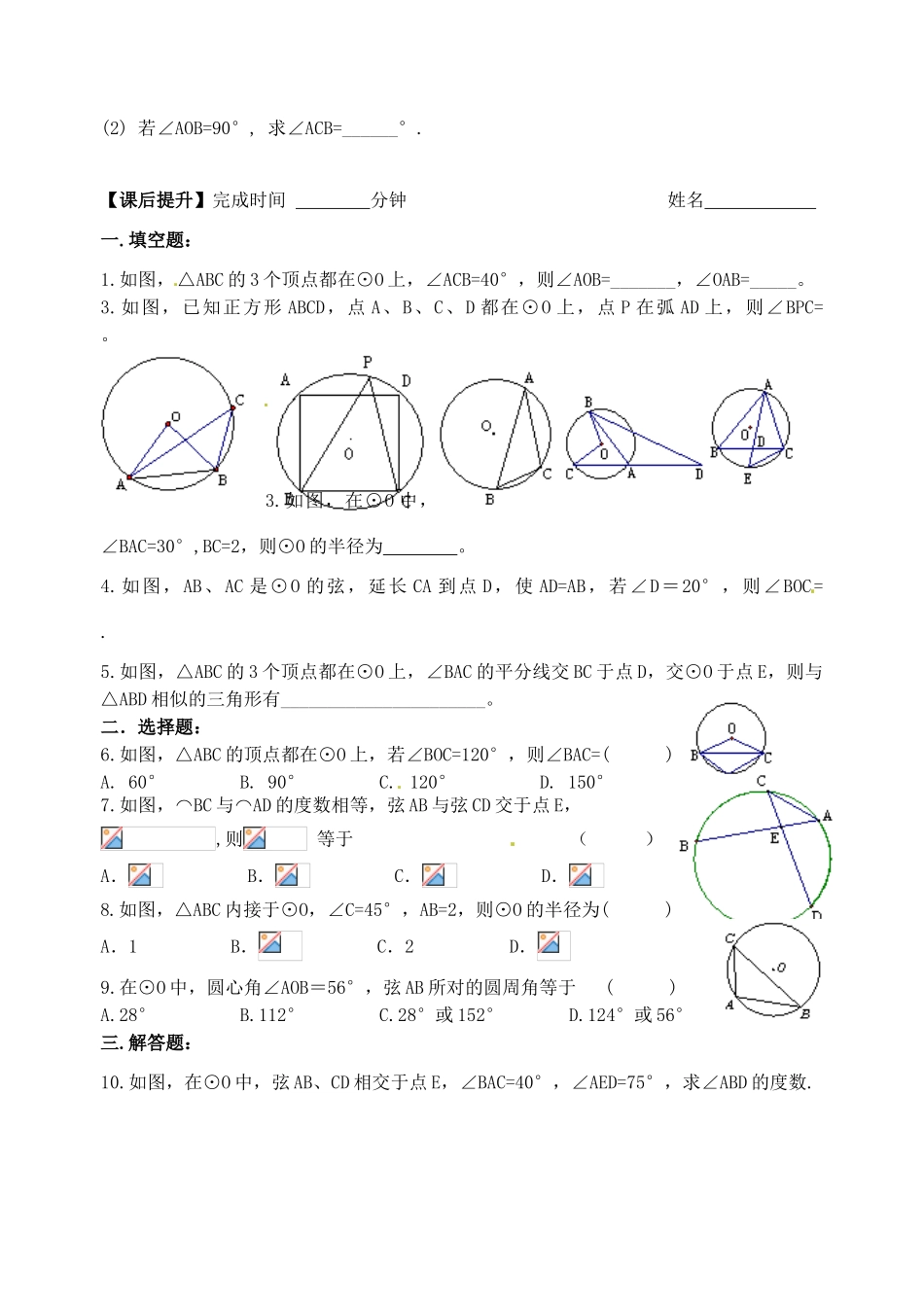
课题:5.3圆周角(1)【学习目标】1.经历探索圆周角的有关性质的过程.2.理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题.【课前预习】活动一操作与思考1.如图,点A在⊙O外,点B1、B2、B3在⊙O上,点C在⊙O内,度量∠A、∠B1、∠B2、∠B3、∠C的大小,你能发现什么?∠B1、∠B2、∠B3有什么共同的特征?。归纳得出结论,顶点在_____,并且两边______________________的角叫做圆周角。强调条件:①_______________________,②___________________________。2.活动二:如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC所对的圆心角、圆周角,求出图(1)、(2)、(3)中∠BAC的度数.(1)∠BAC=°(2)∠BAC=°(3)∠BAC=°通过计算发现:∠BAC=__∠BOC.3.活动三:(1)如图,BC所对的圆心角有多少个?BC所对的圆周角有多少个?请在图中画出BC所对的圆心角和圆周角。答:(2)对于这几种位置关系,结论∠BAC=∠BOC还成立吗?试证明之.通过上述讨论发现:。【学习过程】例1.如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。例2.AC是⊙O的直径,BD是⊙O的弦,EC∥AB,交⊙O于E。图中哪些与∠BOC相等?请分别把它们表示出来并说明理由.【当堂检测】1、下列各图中的角是圆周角的有。(填序号)2、如图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠BAC=350(1)∠BDC=_______°,理由是_____________________.(2)∠BOC=_______°,理由是_____________________.3、如图,点A、B、C在⊙O上,(1)若∠BAC=60°,求∠BOC=______°;(2)若∠AOB=90°,求∠ACB=______°.【课后提升】完成时间分钟姓名一.填空题:1.如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。3.如图,已知正方形ABCD,点A、B、C、D都在⊙O上,点P在弧AD上,则∠BPC=。3.如图,在⊙O中,∠BAC=30°,BC=2,则⊙O的半径为。4.如图,AB、AC是⊙O的弦,延长CA到点D,使AD=AB,若∠D=20°,则∠BOC=.5.如图,△ABC的3个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有______________________。二.选择题:6.如图,△ABC的顶点都在⊙O上,若∠BOC=120°,则∠BAC=()A.60°B.90°C.120°D.150°7.如图,⌒BC与⌒AD的度数相等,弦AB与弦CD交于点E,,则等于()A.B.C.D.8.如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为()A.1B.C.2D.9.在⊙O中,圆心角∠AOB=56°,弦AB所对的圆周角等于()A.28°B.112°C.28°或152°D.124°或56°三.解答题:10.如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.9.如图,点A、B、C、D在⊙O上,∠ADC=∠BDC=60°.判断△ABC的形状,并说明理由.10.如图,在⊙O中,∠BAD=50°,求∠C的大小.11.如图,在⊙O中,⌒DE=2⌒BC,∠EOD=64°,求∠A的度数。12.如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,探索∠ACB与∠BAC之间的数量关系?并说明理由.【中考链接】13.如图,已知⊙O的半径为2,弦BC的长为,点A为弦BC所对优弧上任意一点(B,C两点除外)。⑴求∠BAC的度数;⑵求△ABC面积的最大值.