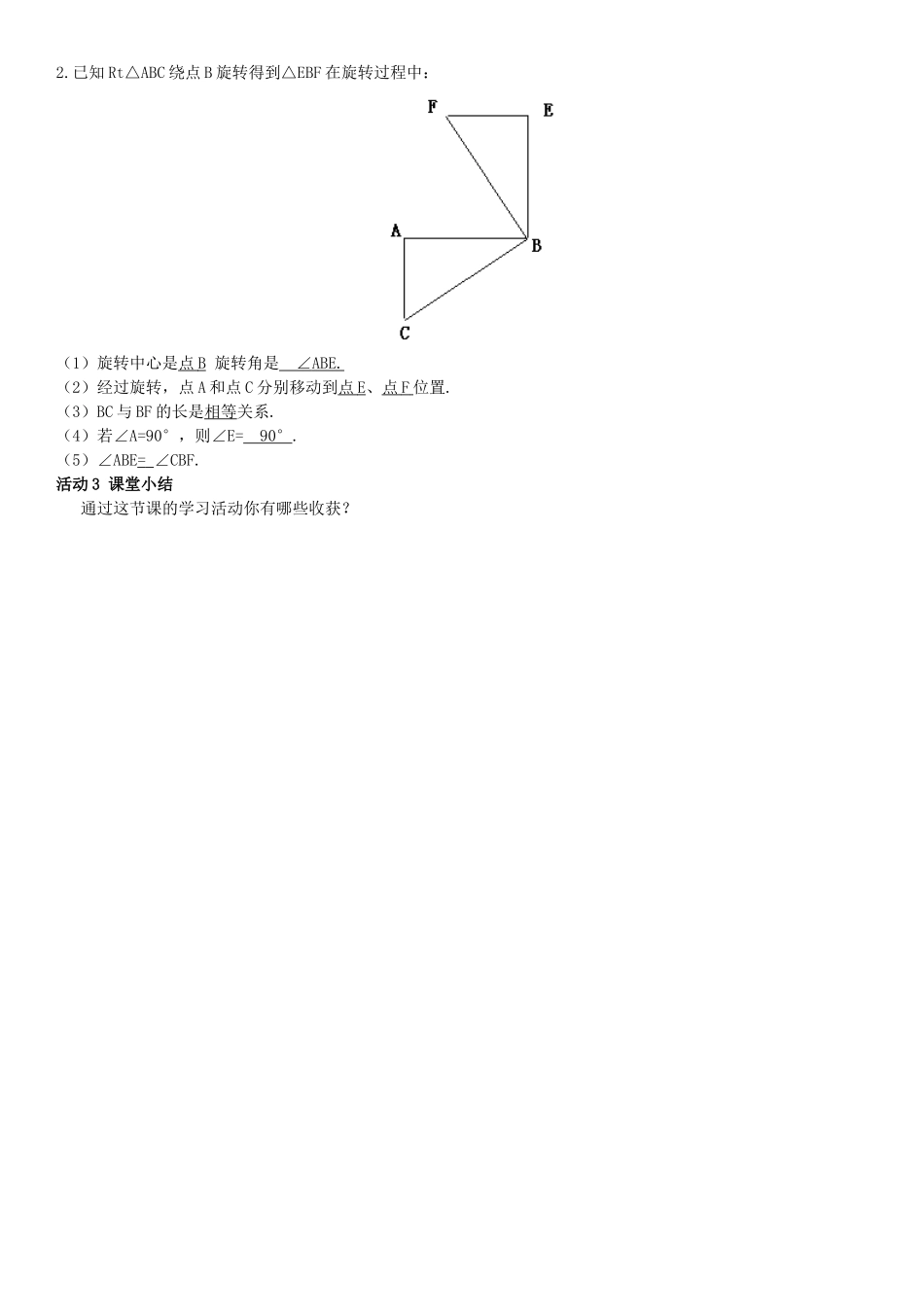
5.2旋转1.掌握旋转、旋转中心和旋转角的概念,并理解旋转的性质.2.能画出简单图形旋转后的对应图形.自学指导阅读课本P119~121,完成下列问题.自学反馈1.将一个平面图形F上的每一个点,绕这个平面内一定点旋转同一个角a,得到图形F′,图形的这种变换就叫作旋转.这个定点叫作旋转中心.角a叫作旋转角.原位置的图形F叫作原像,新位置的图形F′叫作原图形F在旋转下的像.图形F上的每一个点P与它在旋转下的像点P′叫作在旋转下的对应点.2.如图,将△ABC以O为旋转中心旋转60°得到⊿A′B′C′.P点在这个旋转下的像是P′点.图中哪些线段相等?哪些点与旋转中心连线所成的角相等?在游戏过程中,图形的什么发生了变化?什么没有发生变化?解:略.3.旋转是特点与性质:①对应点到旋转中心的距离相等.②对应点与旋转中心的连线所成的角彼此相等,且等于旋转角.③旋转不改变图形的形状和大小.活动1小组讨论例如图,将三角形ABC按逆时针方向旋转45º,得到三角形AB'C'.(1)图中哪一点是旋转中心?(2)∠B'AB和∠C'AC有何关系?它们的度数是多少?(3)AB与AB',AC与AC'有何关系?解:(1)点A是旋转中心.(2)点B与B’,C与C’是对应点.因为两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角,所以∠B'AB=∠C'AC=45°.(3)因为对应点到旋转中心的距离相等,所以AB=AB',AC=AC'.活动2跟踪训练1.将叶片图案旋转180°后,得到的图形是(D).叶片图案ABCD2.已知Rt△ABC绕点B旋转得到△EBF在旋转过程中:(1)旋转中心是点B旋转角是∠ABE.(2)经过旋转,点A和点C分别移动到点E、点F位置.(3)BC与BF的长是相等关系.(4)若∠A=90°,则∠E=90°.(5)∠ABE=∠CBF.活动3课堂小结通过这节课的学习活动你有哪些收获?