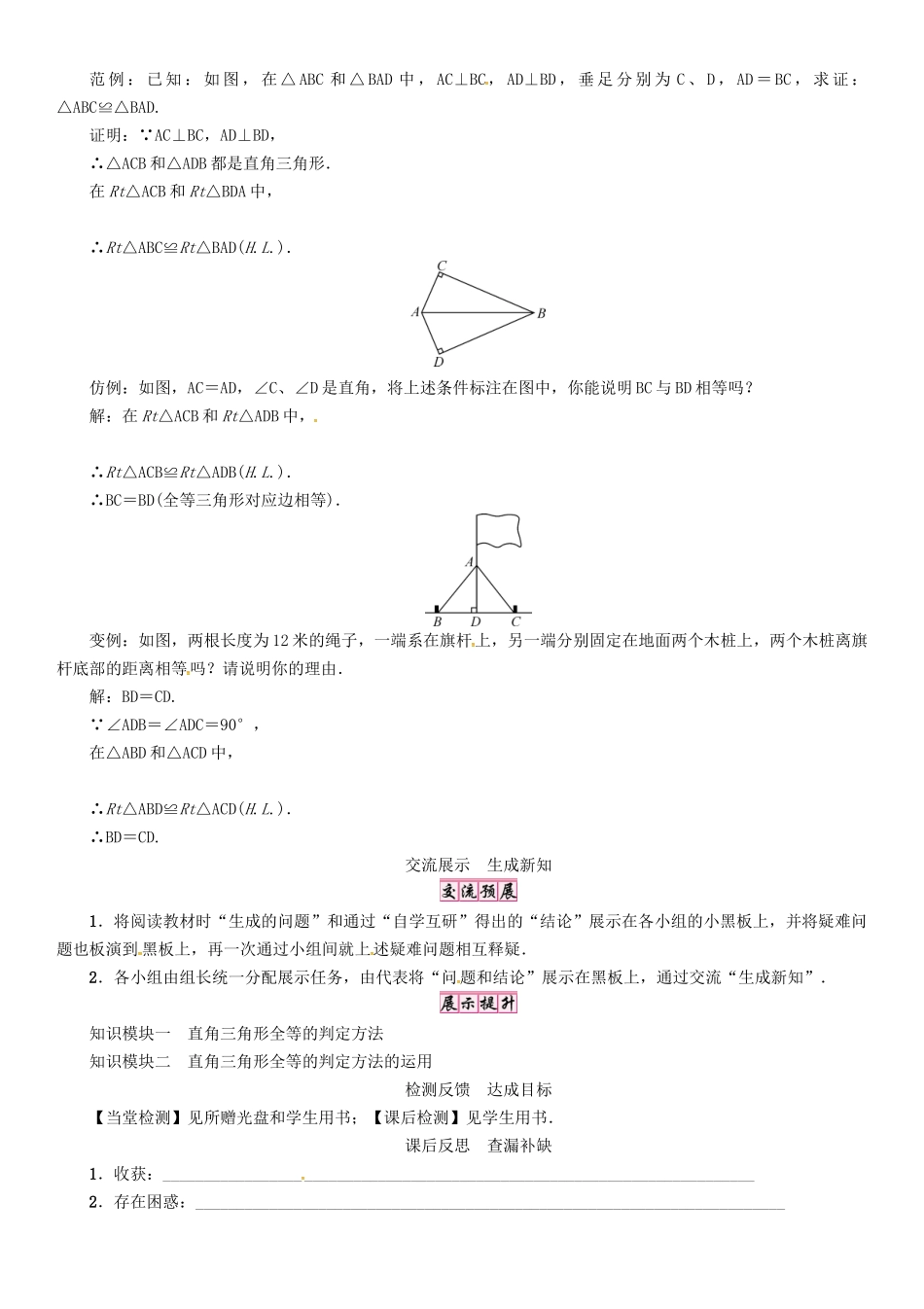
课题斜边直角边【学习目标】1.掌握已知直角三角形的一条直角边和斜边作直角三角形的方法;2.掌握直角三角形全等的判定方法“H.L.”;3.能用直角三角形全等的判定方法解决简单问题.【学习重点】理解利用“斜边直角边”来判定直角三角形全等的方法.【学习难点】灵活运用五种方法(S.A.S.、A.S.A.、A.A.S.、S.S.S.、H.L.)来判定直角三角形全等.行为提示:创景设疑,帮助学生知道本节课学什么.知识链接:已学过的全等判定的方法:S.A.S.、A.S.A.、A.A.S.、S.S.S..情景导入生成问题温故知新(1)判定两个三角形全等的方法:S.A.S.、A.S.A.、A.A.S.、S.S.S.;(2)如图,Rt△ABC中,直角边是AC、BC,斜边是AB;(3)如图,AB⊥BE于B,DE⊥BE于E,①若∠A=∠D,AB=DE,则△ABC与△DEF全等(选填“全等”或“不全等”,下同),根据A.S.A.(用简写法,下同);②若∠A=∠D,BC=EF,则△ABC与△DEF全等,根据A.A.S.;③若AB=DE,BC=EF,则△ABC与△DEF全等,根据S.A.S.;④若AB=DE,BC=EF,AC=DF,则△ABC与△DEF全等,根据S.S.S..(4)对于两个三角形,如果有“边边角”分别对应相等,那么这两个三角形一定全等吗?若不,请举出反例.行为提示:认真阅读课本,独立完成“自学互研”中的题目.自主的完成有关的练习,并在练习中发现规律,从猜测到探索到理解知识.学法指导:直角三角形是特殊三角形,所以不仅有一般三角形判定全等的方法,还有直角三角形特有的判定方法“H.L.”我们应根据具体问题的实际情况选择判定两个直角三角形全等的方法.注意:1.“H.L.”是仅适用于直角三角形的特殊方法;2.注意一组直角边与斜边分别对应相等;3.因为H.L.仅适用于直角三角形,书写格式应为:在Rt△ABC和Rt△DEF中.∴Rt△ABC≌Rt△DEF(H.L.)行为提示:若要利用“H.L.”,则必须根据题意找到相应的条件.行为提示:找出自己不明白的问题,先对学,再群学.充分在小组内展示自己,对照答案,提出疑惑,小组内讨论解决.小组解决不了的问题,写在各小组展示的黑板上,在展示的时候解决.积极发表自己的不同看法和解法,大胆质疑,认真倾听.做每一步运算时都要自觉地注意有理有据.自学互研生成能力阅读教材P73~P75,完成下面的内容:如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?我们可以按下面的方法研究一下.1.动手试一试:根据教材P74画图步骤,完成“做一做”,画一个Rt△ABC,使∠A=90°,一直角边CA=2cm,斜边BC=3cm.2.把你画的三角形跟其他同学画的三角形进行比较,观察是否能够完全重合?归纳:由上面的画图和实验可以得到判定两个直角三角形全等的一个方法.直角三角形全等的条件:斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边直角边”或“H.L.”.3.用数学语言表述上面的判定方法.在Rt△ABC和Rt△A1B1C1中,∴Rt△ABC≌Rt△A1B1C1(H.L.).4.直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:S.A.S.、A.S.A.、A.A.S.、S.S.S.,还有直角三角形特殊的判定方法——“H.L.”.范例:已知:如图,在△ABC和△BAD中,AC⊥BC,AD⊥BD,垂足分别为C、D,AD=BC,求证:△ABC≌△BAD.证明: AC⊥BC,AD⊥BD,∴△ACB和△ADB都是直角三角形.在Rt△ACB和Rt△BDA中,∴Rt△ABC≌Rt△BAD(H.L.).仿例:如图,AC=AD,∠C、∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?解:在Rt△ACB和Rt△ADB中,∴Rt△ACB≌Rt△ADB(H.L.).∴BC=BD(全等三角形对应边相等).变例:如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.解:BD=CD. ∠ADB=∠ADC=90°,在△ABD和△ACD中,∴Rt△ABD≌Rt△ACD(H.L.).∴BD=CD.交流展示生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一直角三角形全等的判定方法知...