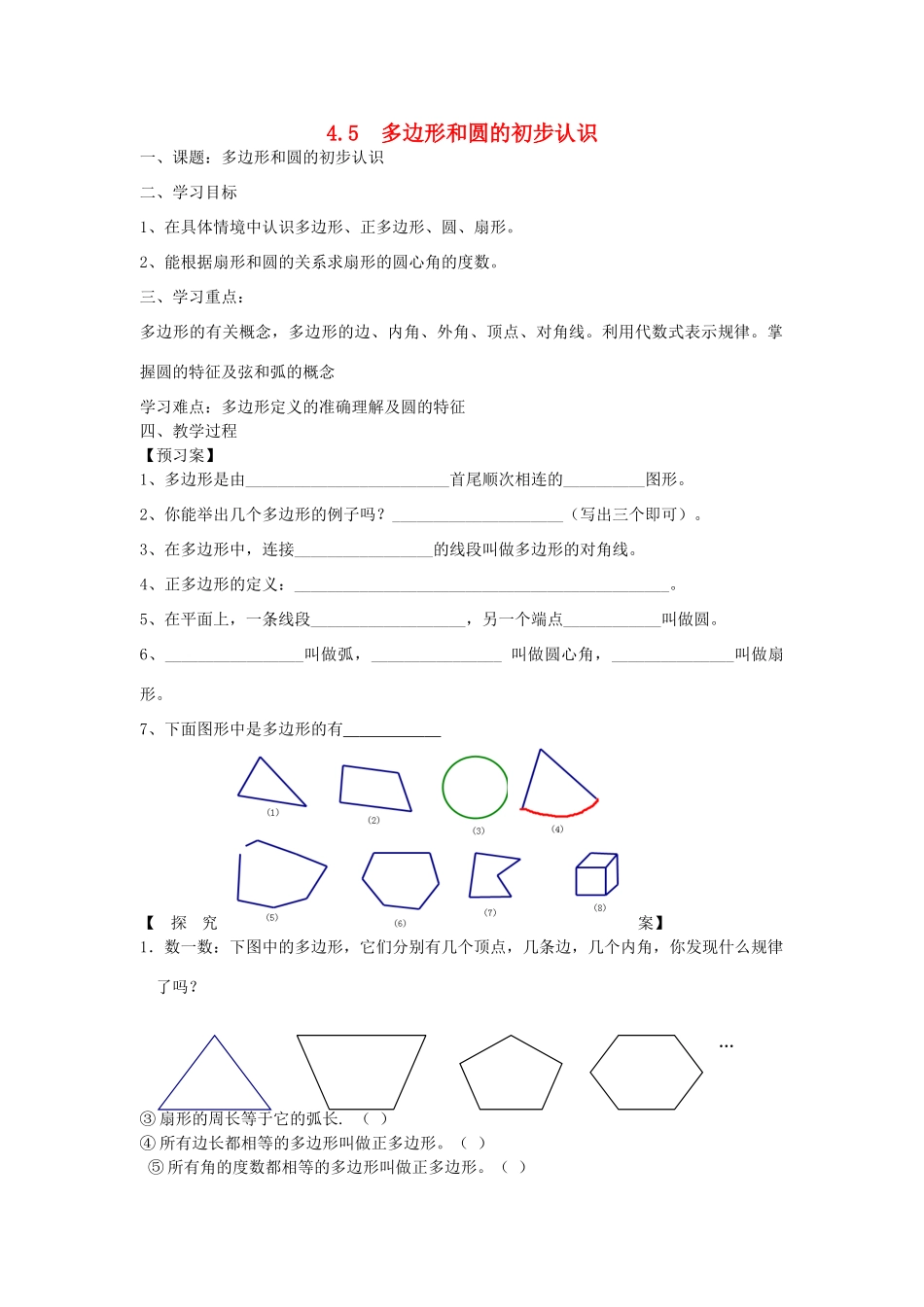
4.5多边形和圆的初步认识一、课题:多边形和圆的初步认识二、学习目标1、在具体情境中认识多边形、正多边形、圆、扇形。2、能根据扇形和圆的关系求扇形的圆心角的度数。三、学习重点:多边形的有关概念,多边形的边、内角、外角、顶点、对角线。利用代数式表示规律。掌握圆的特征及弦和弧的概念学习难点:多边形定义的准确理解及圆的特征四、教学过程【预习案】1、多边形是由_________________________首尾顺次相连的__________图形。2、你能举出几个多边形的例子吗?_____________________(写出三个即可)。3、在多边形中,连接_________________的线段叫做多边形的对角线。4、正多边形的定义:______________________________________________。5、在平面上,一条线段___________________,另一个端点____________叫做圆。6、_________________叫做弧,________________叫做圆心角,_______________叫做扇形。7、下面图形中是多边形的有【探究案】1.数一数:下图中的多边形,它们分别有几个顶点,几条边,几个内角,你发现什么规律了吗?…③扇形的周长等于它的弧长.()④所有边长都相等的多边形叫做正多边形。()⑤所有角的度数都相等的多边形叫做正多边形。()…2.用各种不同的方法把图形分割成三角形,至少可以分割成5个三角形的多边形是()A、五边形B、六边形C、七边形D、八边形3、(1).某多边形从一个顶点出发,分别连结这个点与其余各顶点,可把这个多边形分成8个三角形,则这个多边形是___________.(2).从一个十八边形的某个顶点出发,分别连结这个点与其余各顶点,可以把这个十八边形分割成________个三角形.(3).某多边形的某个顶点出发,可连出12条对角线,则这个多边形有_________条边.4.圆可以分割成若干个扇形。如图,若OA,OB,OC是圆的三条半径,则图中共有个扇形。5、在一个半径为4cm的圆中,有一个圆心角为90°的扇形,请计算这个扇形的面积.【作业】1.下列几何图形中,是平面图形的为__________①三角形,②圆,③圆柱,④圆锥,⑤正方体,⑥扇形。2.四边形切掉一个角后,还有_______________个角。多边形三边形四边形五边形六边形…n边形顶点数边数内角数思考:若一个多边形有12个内角,则这个多边形为()边形,若一个多边形有20个顶点,则这个多边形为()边形.2、从一个四边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个四边形分成_______个三角形。若是一个五边形,可以分割成_______个三角形。若是六边形可以分割成______个三角形,若是一个n边形,可以分割成_______个三角形。多边形四边形五边形六边形…n边形过点A对角线条数分成三角形个数【训练案】1、判断题①扇形是圆的一部分.()②圆的一部分是扇形.()3.判断题①扇形是圆的一部分。()②圆的一部分是扇形。()③扇形的周长等于它的弧长。()④所有边长都相等的多边形叫做正多边形。()⑤所有角的度数都相等的多边形叫做正多边形。()4.若一个正六边形的边长是4,则它的周长是_____。5.从十边形的某个顶点出发,连出的对角线的条数是________6.一个扇形的圆心角为144度,则该扇形的面积是整个圆面积的_______7.若在n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?8.若点P在多边形的一条边上(不是顶点),再将点P与n边形各顶点连接起来,可将多边形分割成多少个三角形?9、在一个半径为4cm的圆中,有一个圆心角为90°的扇形,请计算这个扇形的面积.10.将一个圆分割成三个扇形,他们的圆心角度数比为1:2:3;4,求这四个圆心角的度数。课后反思