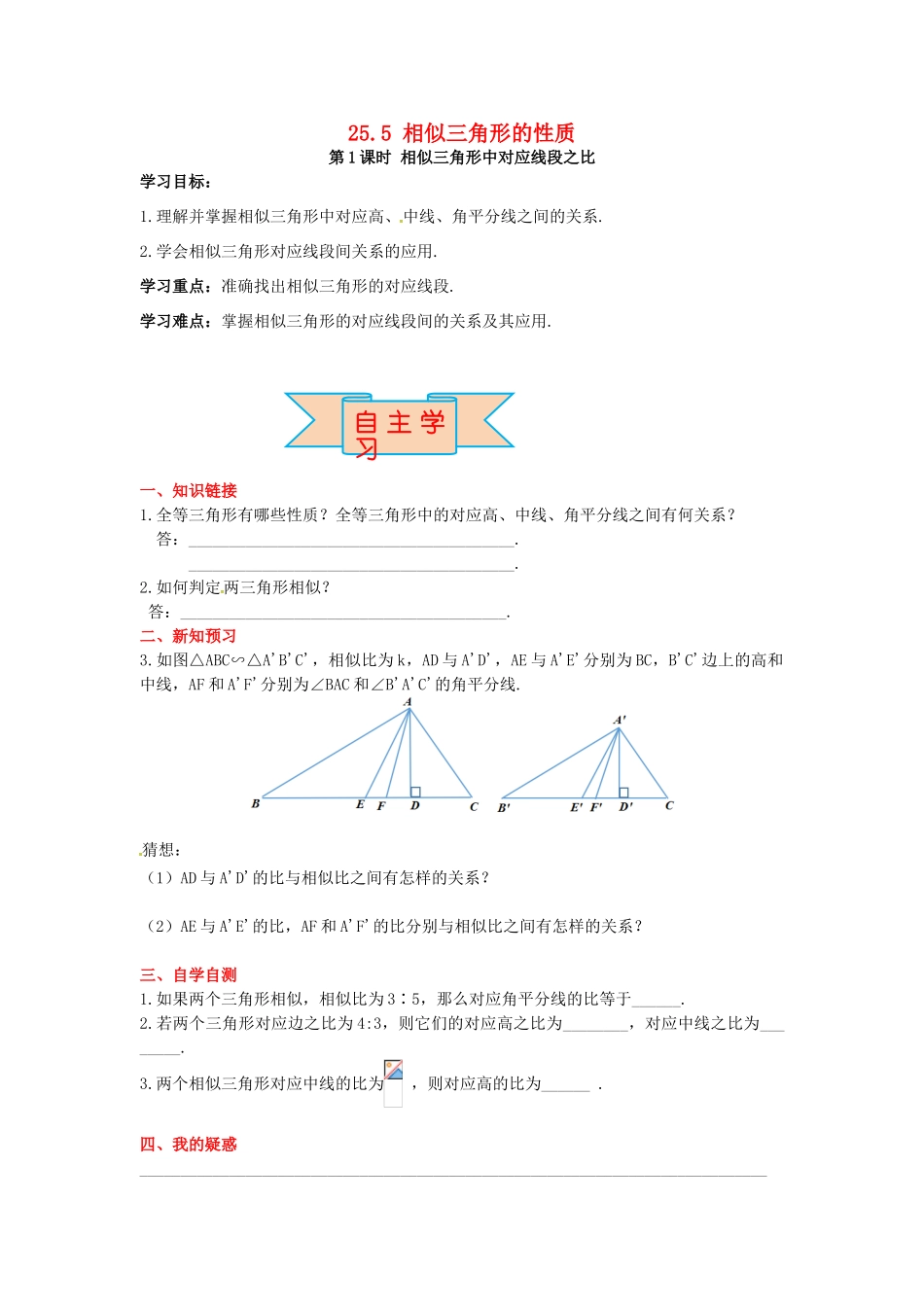
25.5相似三角形的性质第1课时相似三角形中对应线段之比学习目标:1.理解并掌握相似三角形中对应高、中线、角平分线之间的关系.2.学会相似三角形对应线段间关系的应用.学习重点:准确找出相似三角形的对应线段.学习难点:掌握相似三角形的对应线段间的关系及其应用.一、知识链接1.全等三角形有哪些性质?全等三角形中的对应高、中线、角平分线之间有何关系?答:________________________________________.________________________________________.2.如何判定两三角形相似?答:________________________________________.二、新知预习3.如图△ABC∽△A'B'C',相似比为k,AD与A'D',AE与A'E'分别为BC,B'C'边上的高和中线,AF和A'F'分别为∠BAC和∠B'A'C'的角平分线.猜想:(1)AD与A'D'的比与相似比之间有怎样的关系?(2)AE与A'E'的比,AF和A'F'的比分别与相似比之间有怎样的关系?三、自学自测1.如果两个三角形相似,相似比为3∶5,那么对应角平分线的比等于______.2.若两个三角形对应边之比为4:3,则它们的对应高之比为________,对应中线之比为________.3.两个相似三角形对应中线的比为,则对应高的比为______.四、我的疑惑_____________________________________________________________________________自主学习_______________________________________________________________________________________________________________________________________________________一、要点探究探究点1:相似三角形的性质定理【证明猜想】已知,如图,△ABC∽△A′B′C′,相似比为k,(1)AD、A′D′分别为BC,B′C′边上的高,求证:=k.(提示:运用两角对应相等先证△ABD∽△A′B′D′)(2)AE、A′E′分别为BC,B′C′边上的中线,求证:=k.(提示:运用两边对应成比例且夹角相等先证△ABE∽△A′B′E′)(3)AF、A′F′分别为∠BAC,∠B′A′C′的角平分线.求证:=k.【归纳】相似三角形的性质定理:相似三角形对应高的比、对应中线的比、对应角平分线的比,都等于相似比.(一)相似三角形对应高的比等于相似比例1:已知:如图,△ABC中,DE∥BC,AH⊥BC于点H,AH交DE于点G.已知DE=10,BC=15,AG=12.求GH的值.【归纳总结】利用相似三角形的性质:对应高的比等于相似比,将所求线段转化为求对应高的差.【针对训练】1.如图,CD是Rt△ABC的斜边AB上的高.合作探究(1)则图中有几对相似三角形.(2)若AD=9cm,CD=6cm,求BD.(3)若AB=25cm,BC=15cm,求BD.(二)相似三角形对应角平线的比等于相似比例2:已知两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?【归纳总结】在利用相似三角形的性质解题时,一定要注意“对应”二字,只有对应线段的比才等于相似比,而相似比即为对应边的比,列比例式时,尽可能回避复杂方程的变形.(三)相似三角形对应中线的比等于相似比例3:已知△ABC∽△A′B′C′,=,AB边上的中线CD=4cm,求A′B′边上的中线C′D′.【归纳总结】相似三角形对应中线的比等于相似比.【针对训练】2.若△ABC∽△A′B′C′,BC=3.6cm,B′C′=6cm,AE是△ABC的一条中线,AE=2.4cm,则△A′B′C中对应中线A′E′的长是.二、课堂小结相似三角形的性质1内容基本图形内容相似三角形对应高的比、对应中线的比、对应角平分线的比,都等于_________解题策略利用相似三角形的性质解题时,一定要注意“对应”二字,只有对应线段的比才等于相似比,而相似比即为对应边的比,列比例式时,尽可能回避复杂方程的变形.1.若两个相似三角形的相似比是2∶3,则它们的对应高的比是,对应中线的比是,对应角平分线的比是.2.如图,△ADE∽△ABC,相似比为2:5,则AF:AG=____________.3.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,它在暗盒中所成像CD的高为16cm,则暗盒宽为_____cm.4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.当堂检测当堂检测参考答案:1.2∶32∶32∶32.2:53.204.解:∵△ABC∽△DEF,解得,EH=3.2(cm).