九年级数学上册 28.3 第3课时 圆内接四边形导学案 （新版）冀教版-（新版）冀教版初中九年级上册数学学案VIP免费

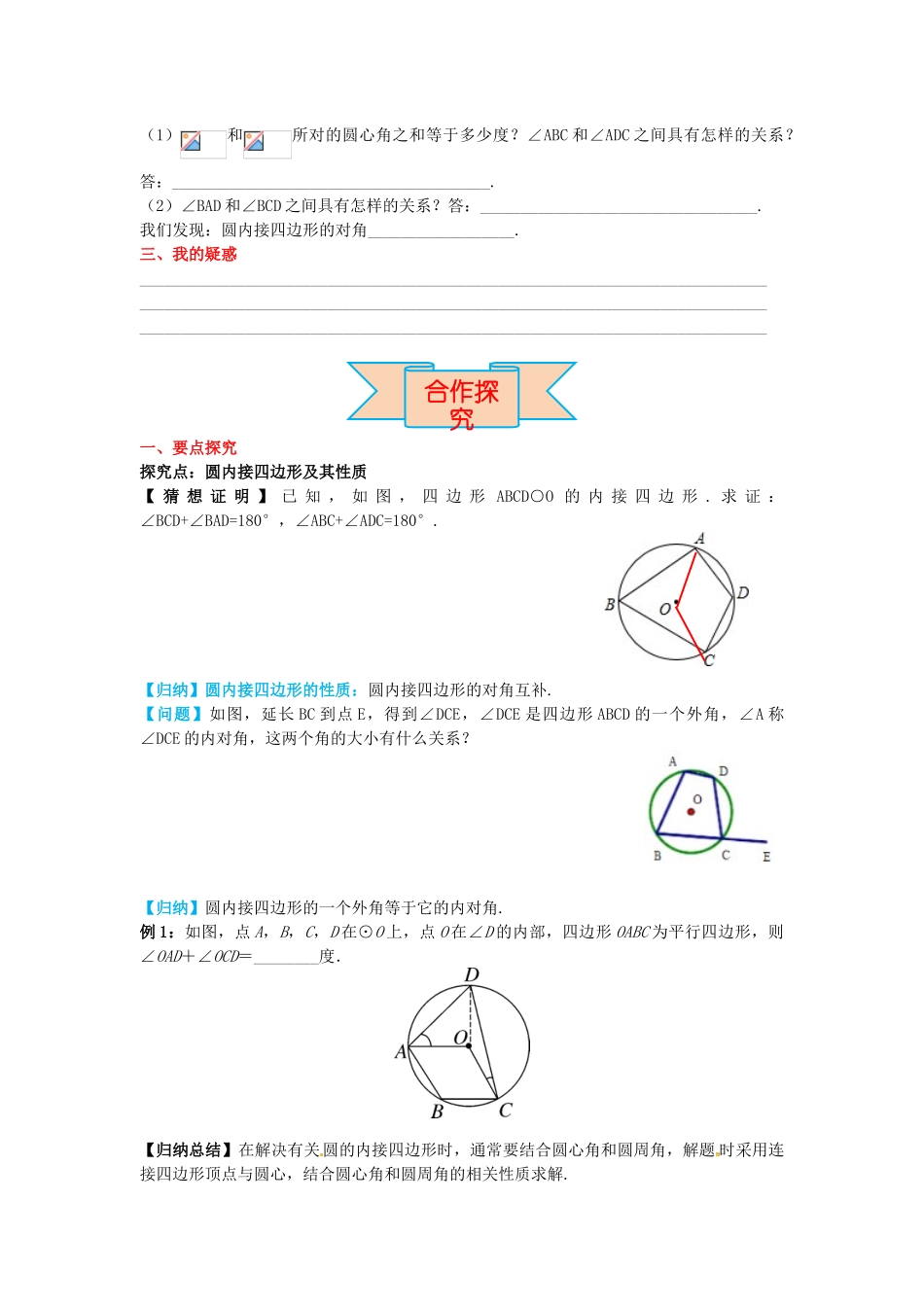
28.3圆心角和圆周角第3课时圆内接四边形学习目标：理解并掌握圆内接四边形的概念及性质并学会运用学习重点：圆周角的性质.学习难点：圆周角的性质及计算.一、知识链接1.如图1，△ABC叫O的________三角形，O叫△ABC的_______圆.2.如图1，若的度数为100°，则∠BOC=______，∠A=______.3.如图2，在四边形ABCD中，∠B与∠1互补，AD的延长线与DC所夹∠2=60°，则∠1=______,∠B=_______.4.如图，劣弧AB所对的圆心角为α，优弧ADB所对的圆心角为α，根据周角的定义，可得α+β=________°.图1图2图3二、新知预习5.我们已经学习过圆与三角形，现在我们探究四边形与圆的关系.【概念学习】四个顶点都在同一个圆上的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.6.圆内接四边形的角度间有哪些关系呢？用量角器量一量，并作猜想.自主学习（1）和所对的圆心角之和等于多少度？∠ABC和∠ADC之间具有怎样的关系？答：_______________________________________.（2）∠BAD和∠BCD之间具有怎样的关系？答：__________________________________.我们发现：圆内接四边形的对角__________________.三、我的疑惑_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________一、要点探究探究点：圆内接四边形及其性质【猜想证明】已知，如图，四边形ABCD○O的内接四边形.求证：∠BCD+∠BAD=180°，∠ABC+∠ADC=180°.【归纳】圆内接四边形的性质：圆内接四边形的对角互补.【问题】如图，延长BC到点E，得到∠DCE，∠DCE是四边形ABCD的一个外角，∠A称∠DCE的内对角，这两个角的大小有什么关系？【归纳】圆内接四边形的一个外角等于它的内对角.例1：如图，点A，B，C，D在⊙O上，点O在∠D的内部，四边形OABC为平行四边形，则∠OAD＋∠OCD＝________度．【归纳总结】在解决有关圆的内接四边形时，通常要结合圆心角和圆周角，解题时采用连接四边形顶点与圆心，结合圆心角和圆周角的相关性质求解.合作探究例2：如图，已知A，B，C，D是⊙O上的四点，延长DC，AB相交于点E.若BC＝BE.求证：△ADE是等腰三角形．【归纳总结】在证明与内接四边形有关的问题时，要时刻牢记其性质：圆内接四边形内角互补.【针对训练】1.圆内接四边形ABCD中，已知∠A=70°，则∠C=（）A．20°B．30°C．70°D．110°2.如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，则∠BCD的度数是（）A．88°B．92°C．106°D．136°3.如图，四边形ABCD是⊙O的内接四边形，∠B=70°，则∠D的度数是（）A．110°B．90°C．70°D．50°4.四边形ABCD为圆O的内接四边形，已知∠BOD=100°，则∠BCD=．5.如图，已知四边形ABCD内接于⊙O，点O在∠D的内部，∠OAD+∠OCD=50°，则∠B=．6.如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．（1）若∠E=∠F时，求证：∠ADC=∠ABC；（2）若∠E=∠F=42°时，求∠A的度数；（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．二、课堂小结圆内接四边形内容概念四个顶点都在同一个圆上的四边形叫做圆内接四边形，这个圆叫做四边形的___圆性质（1）圆内接四边形的对角__________________.（2）圆内接四边形的一个外角等于四边的内对角.1.如图，四边形ABCD内接于半圆O，已知∠ADC=140°，则∠AOC的大小是（）A．40°B．60°C．70°D．80°第1题图第2题图第3题图2.如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（）A．45°B．50°C．60°D．75°3.如图，在⊙O中，∠AOC=140°，∠ACB=50°，则∠BAC=．4.四边形ABCD为圆O的内接四边形，已知∠BOD=100°，则∠BCD=．5.已知四边形ABCD顶点都在4×4的正方形网格格点上，如图所示，（1）请画出四边形ABCD的外接圆，并标明圆心M的位置；（2）这个圆中弦BC所对的圆周角的度数是．当堂检测6.如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F．（1）若∠E+∠F=α，求∠A的度数（用含α的式子表示）；（2）若∠E+∠F=60°，求∠A的度数．当堂检测参考答案：1.D2.C3.20°4.130°或50°5.（1）（2）45°6.（1）∵四边形ABCD为⊙O的内接四边形，∴∠A=∠BCF，∵∠EBF=∠A+∠E，而∠EBF=180°﹣∠BCF﹣∠F，∴∠A+∠E=180°﹣∠BCF﹣∠F，∴∠A+∠E=180﹣∠A﹣∠F，即2∠A=180°﹣（∠E+∠F），∵∠E+∠F=α，∴∠A=90°﹣α；（2）当α=60°时，∠A=90°﹣×60°=60°．