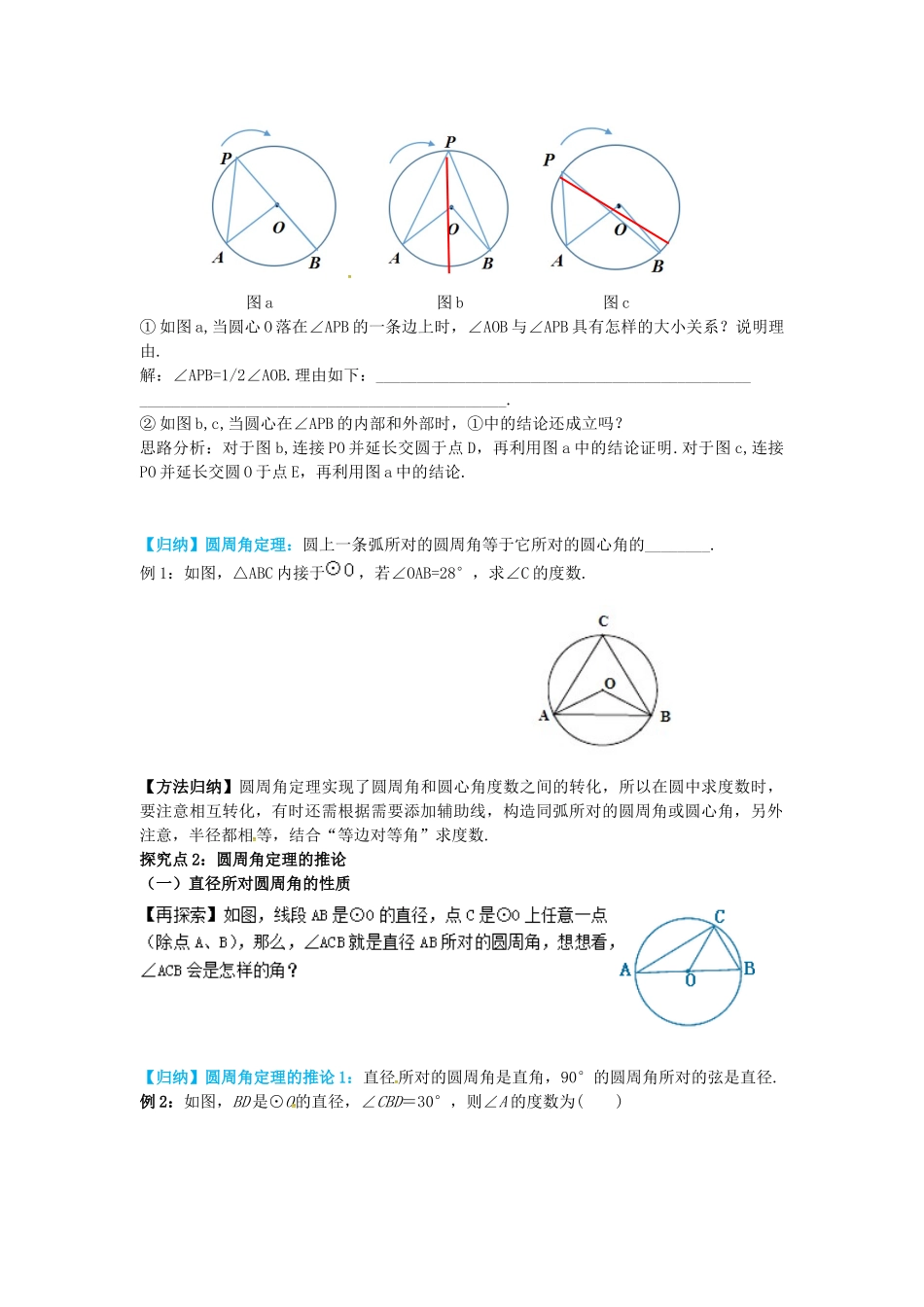
28.3圆心角和圆周角第2课时圆周角学习目标:1.理解圆周角的概念并会判断圆周角.理解并掌握圆周角的性质并进行计算.学习重点:圆周角的性质.学习难点:圆周角的性质及计算.一、知识链接1.圆心角的定义:圆心角是指_________________________________________的角.2.圆心角的性质:在同圆或等圆中,相等的弧或弦所对的圆心角________.2.直角三角形斜边中线的性质:直角三角形斜边上的中线等于斜边的_______.它的逆命题是:如果一个三角形中一边上的中线等于这条边的一半,那么这个三角形是_____三角形,这个逆命题是真命题.二、新知预习2.如图,我们已将知道图①④中的角是圆心角,那么另外两图中的角呢?【概念归纳】顶点在圆上,两边都与圆相交的角叫作圆周角.图_____的角是圆周角.3.如图,写出弧AC所对应的圆周角____________.你还能再做出弧AC对应的圆周角吗?【归纳】同一条弧所对应的圆周角有_____个.4.上图中,作出弧AC对应的圆心角,用量角器量一量,∠AOC与三个圆周角∠B、∠D、∠E的等量关系.自主学习【结论】∠B=∠D=∠E=______∠AOC.三、自学自测1.在⊙O中,所对的圆心角有_____个,所对的圆周角有______个;弦AB所对的圆心角有_____个,弦AB所对的圆周角有_____个。2.如图,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是()A.156°B.78°C.39°D.12°四、我的疑惑_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________一、要点探究探究点1:圆周角的定义及性质(一)圆周角的定义【练一练】指出图中的圆周角.【归纳总结】一个角是圆周角,必须同时满足定义中的两个条件.(二)圆周角的定理【探究】如图,∠AOB和∠APB分别是弧AB所对的圆心角和圆周角.(1)当点P在圆上按照顺时针方向移动时(点P与点B不重合,按照圆心O和圆周角的位置关系,可以分为几种不同情形?说出你的判断并画出相应的图形.答:如图,分为以下三种情形.合作探究图a图b图c①如图a,当圆心O落在∠APB的一条边上时,∠AOB与∠APB具有怎样的大小关系?说明理由.解:∠APB=1/2∠AOB.理由如下:___________________________________________________________________________________________.②如图b,c,当圆心在∠APB的内部和外部时,①中的结论还成立吗?思路分析:对于图b,连接PO并延长交圆于点D,再利用图a中的结论证明.对于图c,连接PO并延长交圆O于点E,再利用图a中的结论.【归纳】圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的________.例1:如图,△ABC内接于,若∠OAB=28°,求∠C的度数.【方法归纳】圆周角定理实现了圆周角和圆心角度数之间的转化,所以在圆中求度数时,要注意相互转化,有时还需根据需要添加辅助线,构造同弧所对的圆周角或圆心角,另外注意,半径都相等,结合“等边对等角”求度数.探究点2:圆周角定理的推论(一)直径所对圆周角的性质【归纳】圆周角定理的推论1:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.例2:如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为()A.30°B.45°C.60°D.75°【针对训练】1.如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数为()A.90°B.60°C.45°D.30°(二)同弧所对圆周角的性质【探究】如图,∠B、∠D、∠E是弧AC所对的圆周角,通过前面的测量,我们知道∠B=∠D=∠E.你能证明这个结论吗?思路分析:连接AO,CO构造出弧AC所对应的圆心角,则通过同弧所对的圆周角等于圆心角的一半,即可得证.【归纳】同弧或等弧所对的圆周角相等.例1:如图,在⊙O中,AB=AC,∠A=30°,则∠B=()A.150°B.75°C.60°D.15°【归纳总结】解题的关键是掌握在同圆或等圆中,相等的两条弧所对的圆周角也相等.注意方程思想的应用.二、课堂小结内容运用策略概念顶点在_______,两边都与圆_____的角叫作圆周角.一个角是圆周角,必须同时满足定义中的两个条件.圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的________.由于...