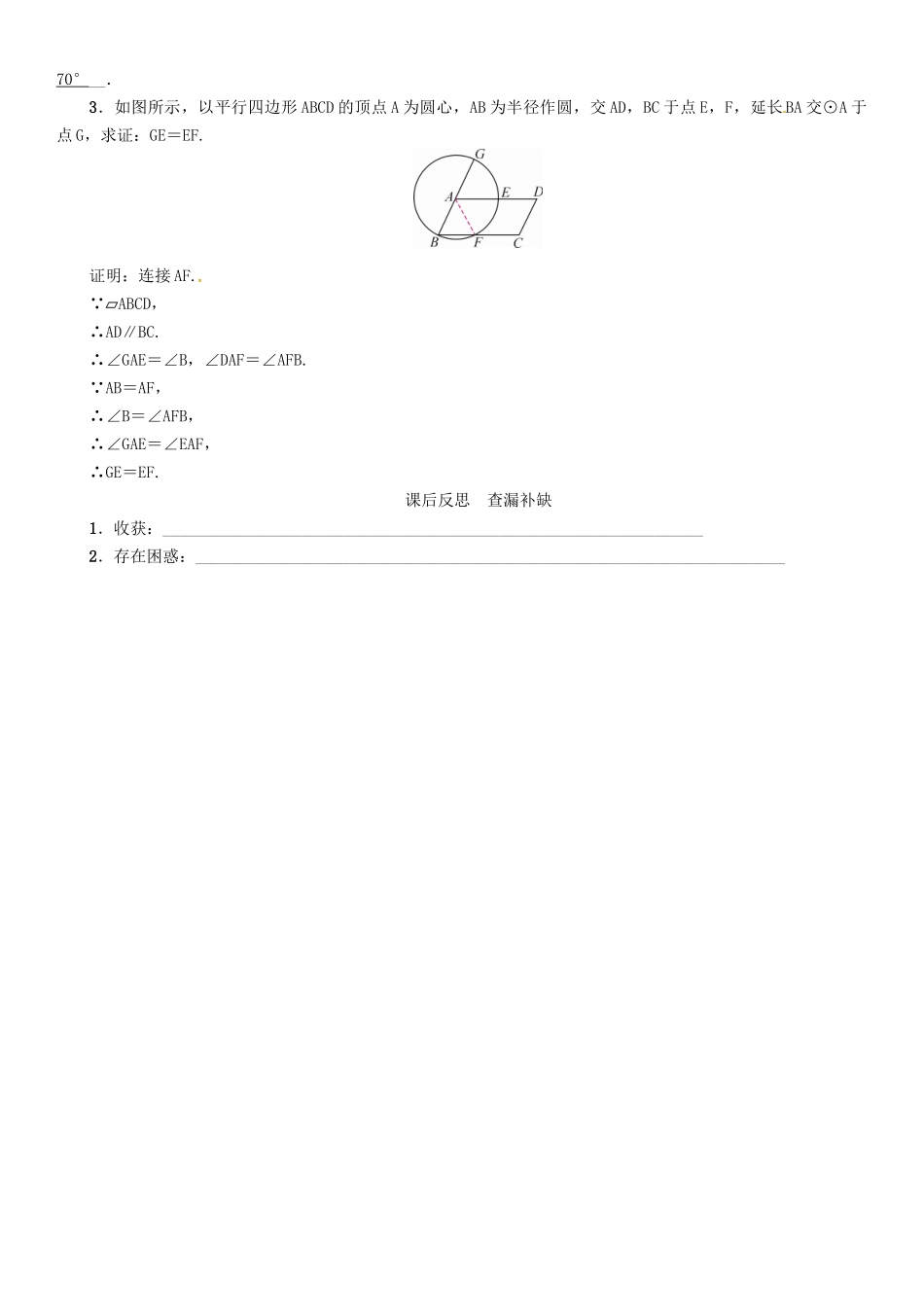
课题:圆心角【学习目标】1.理解并掌握圆心角的概念.掌握圆心角与弧及弦的关系定理.2.通过对圆心角的概念及定理的探究,从而认识到几何中不同量之间的对等关系.【学习重点】弧、弦、圆心角之间关系的定理及推论和它们的应用.【学习难点】探索定理和推论及其应用.情景导入生成问题旧知回顾:1.圆的对称性是怎样的?答:圆是中心对称图形,圆心是它的对称中心.圆是轴对称图形,任意一条直径所在直线都是它的对称轴.圆还具有任意旋转对称性.2.如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=__24°__.自学互研生成能力阅读教材P47~P48,完成下列问题:什么叫圆心角?答:顶点在圆心,角的两边与圆相交,像这样的角叫圆心角.【例1】下列图形中表示的角是圆心角的是(A),A),B),C),D)【变例1】如图所示,__∠COD,∠AOD__是圆心角.(变例1图)(变例2图)【变例2】如图,已知AB为⊙O的直径,点D为半圆周上的一点,且AD所对圆心角的度数是BD所对圆心角度数的两倍,则圆心角∠BOD的度数为__60°__.在同圆或等圆中,圆心角、弧、弦之间关系是怎样的?答:在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等,在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.【例2】如图,在⊙O中,点C是AB的中点,∠A=40°,则∠BOC等于(B)A.40°B.50°C.70°D.80°【变例1】如图,已知在⊙O中,BC是直径,AB=DC,∠AOD=80°,则∠ABC等于(B)A.40°B.65°C.100°D.105°(变例1图)(变例2图)【变例2】如图所示,在⊙O中,AB=AC,∠B=70°,则∠A=__40°__.【变例3】一条弦把圆分成1∶3两部分,则弦所对的圆心角为__90__°.【变例4】⊙O的半径为5cm,弦AB所对的劣弧是⊙O的,则弦AB=__5__cm.【变例5】如图,AB为⊙O的直径,C,D是⊙O上的两点,∠BAC=20°,AD=CD,则∠DAC的度数是(B)A.30°B.35°C.45°D.70°交流展示生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的结论展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一圆心角的概念知识模块二圆心角、弧、弦之间的关系检测反馈达成目标1.如图,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,CD=CE,则下列结论正确的是(B)A.AC>CBB.AC=CBC.AC