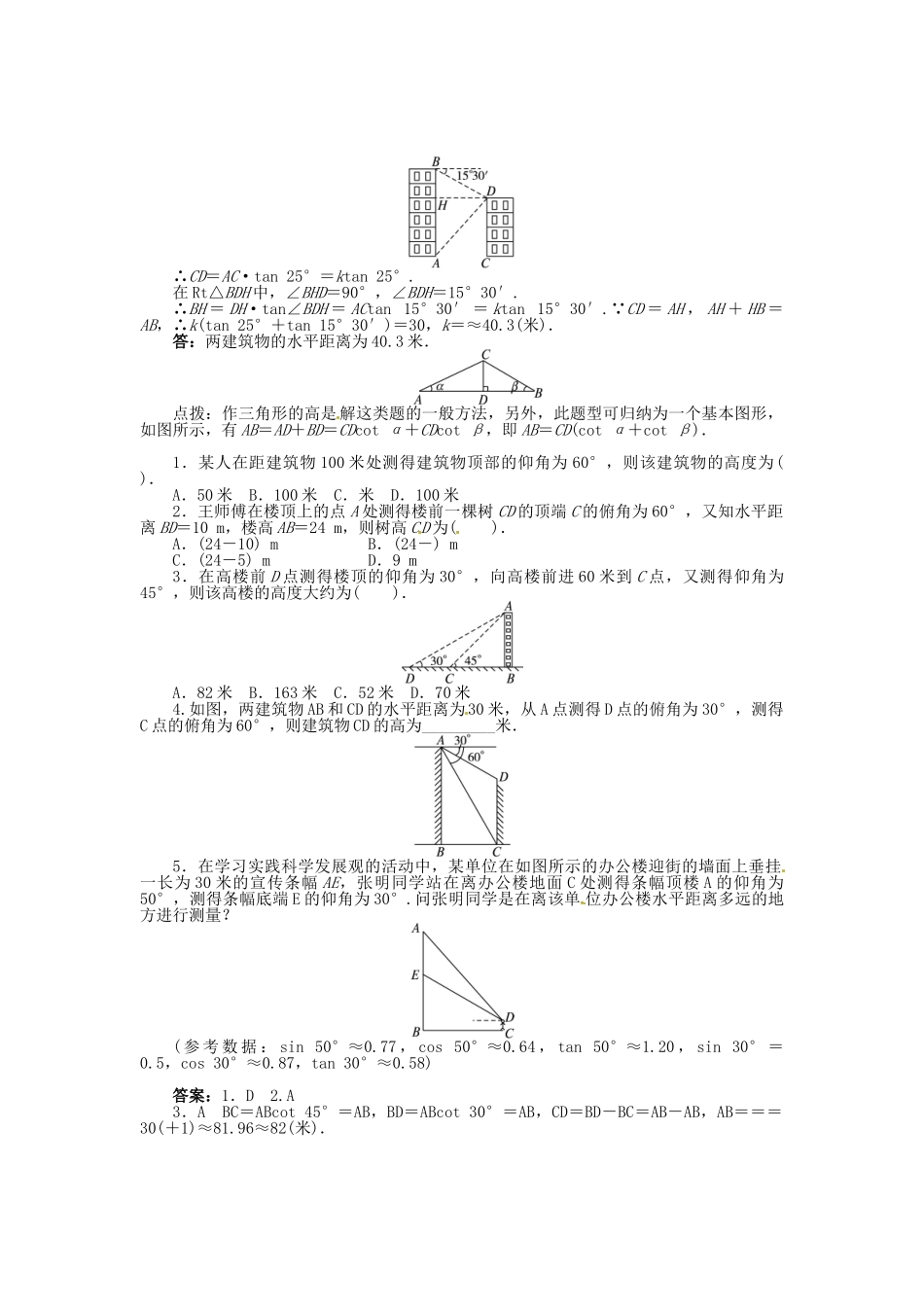
第2课时解直角三角形的应用(一)学前温故解直角三角形,只有下面两种情况:(1)已知两条边;(2)已知一条边和一个______.新课早知1.在进行测量时,从下向上看,视线与水平线的夹角叫做________;从上往下看,视线与水平线的夹角叫做________.2.小晴在地上与楼上窗口的小文说话,小晴的仰角为72°,则小文看小晴().A.俯角为72°B.仰角为72°C.俯角为18°D.仰角为18°3.雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139米的C处(C与塔底B在同一水平线上),用高1.4米的测角仪CD测得塔顶A的仰角α=43°(如图),求这座“千年塔”的高度AB(结果精确到0.1米).(参考数据:tan43°≈0.9325,cot43°≈1.0724)答案:学前温故(2)锐角新课早知1.仰角俯角2.A3.解:在Rt△ADE中,∠α=43°,DE=CB=139米.∵=tanα,∴AE=DE·tanα=139×tan43°=139×0.9325≈129.62.∴AB=AE+EB=129.62+1.4≈131.0(米).与俯角、仰角有关的实际问题【例题】已知如图,八年级(1)班数学兴趣小组为了测量河岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶点D的仰角为25°,然后爬到建筑物AB的顶点B处测得建筑物CD顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)分析:在解决实际问题时,要找出已知条件比较集中的直角三角形,然后通过边角转换,求出有关的未知元素,同时应注意把几何中的有关定理和代数中解方程的思想结合起来解直角三角形.解:过D作DH⊥AB,垂足为H,设AC=k,在Rt△ACD中,∠ACD=90°,∠DAC=25°,∴CD=AC·tan25°=ktan25°.在Rt△BDH中,∠BHD=90°,∠BDH=15°30′.∴BH=DH·tan∠BDH=ACtan15°30′=ktan15°30′.∵CD=AH,AH+HB=AB,∴k(tan25°+tan15°30′)=30,k=≈40.3(米).答:两建筑物的水平距离为40.3米.点拨:作三角形的高是解这类题的一般方法,另外,此题型可归纳为一个基本图形,如图所示,有AB=AD+BD=CDcotα+CDcotβ,即AB=CD(cotα+cotβ).1.某人在距建筑物100米处测得建筑物顶部的仰角为60°,则该建筑物的高度为().A.50米B.100米C.米D.100米2.王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD=10m,楼高AB=24m,则树高CD为().A.(24-10)mB.(24-)mC.(24-5)mD.9m3.在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为().A.82米B.163米C.52米D.70米4.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_________米.5.在学习实践科学发展观的活动中,某单位在如图所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE,张明同学站在离办公楼地面C处测得条幅顶楼A的仰角为50°,测得条幅底端E的仰角为30°.问张明同学是在离该单位办公楼水平距离多远的地方进行测量?(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,sin30°=0.5,cos30°≈0.87,tan30°≈0.58)答案:1.D2.A3.ABC=ABcot45°=AB,BD=ABcot30°=AB,CD=BD-BC=AB-AB,AB===30(+1)≈81.96≈82(米).4.205.解法一:过D作DF⊥AB于F点,在Rt△DFE中,设EF=x米,则DF=x米.在Rt△ADF中,tan50°==1.20,30+x=x×1.20,x≈27.8(米).∴DF=x≈48(米).答:张明同学站在离办公楼水平距离约48米处进行测量的.解法二:过点D作DF⊥AB于F点.在Rt△DFE中,EF=FD·tan30°,在Rt△AFD中,AF=FD·tan50°.∵AE+EF=AF,∴30+FD·tan30°=FDtan50°.∴FD≈48(米).答:张明同学站在离办公楼约48米处进行测量的.