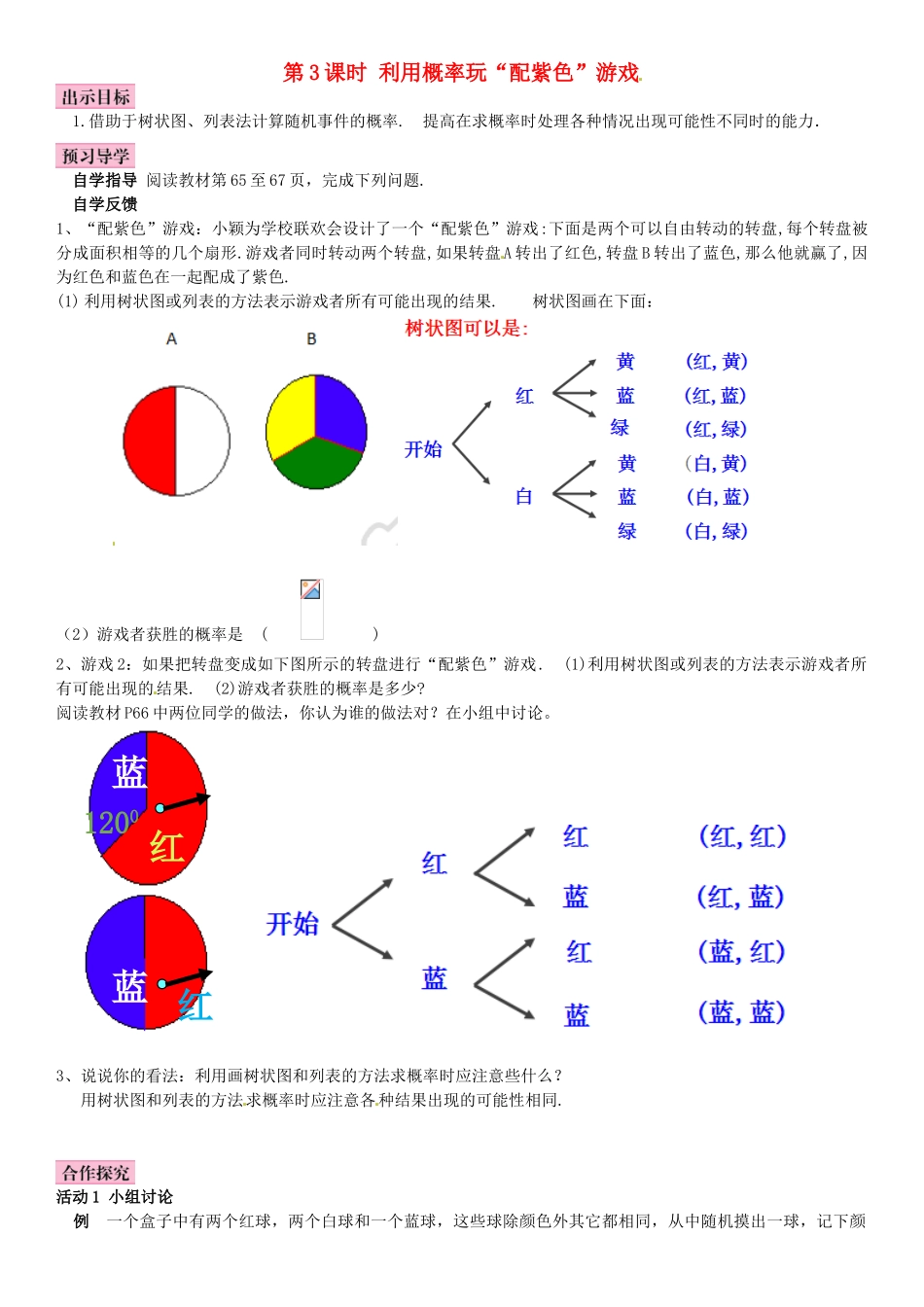
第3课时利用概率玩“配紫色”游戏1.借助于树状图、列表法计算随机事件的概率.提高在求概率时处理各种情况出现可能性不同时的能力.自学指导阅读教材第65至67页,完成下列问题.自学反馈1、“配紫色”游戏:小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.树状图画在下面:(2)游戏者获胜的概率是()2、游戏2:如果把转盘变成如下图所示的转盘进行“配紫色”游戏.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少?阅读教材P66中两位同学的做法,你认为谁的做法对?在小组中讨论。3、说说你的看法:利用画树状图和列表的方法求概率时应注意些什么?用树状图和列表的方法求概率时应注意各种结果出现的可能性相同.活动1小组讨论例一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜1200红红蓝蓝色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率.把两个红球记为红1、红2;两个白球记为白1、白2.则列表格如下:红1红2白1白2蓝红1(红1,红1)(红1,红2)(红1,白1)(红1,白2)(红1,蓝)红2(红2,红1)(红2,红2)(红2,白1)(红2,白2)(红2,蓝)白1(白1,红1)(白1,红2)(白1,白1)(白1,白2)(白1,蓝)白2(白2,红1)(白2,红2)(白2,白1)(白2,白2)(白2,蓝)蓝(蓝,红1)(蓝,红2)(蓝,白1)(蓝,白2)(蓝,蓝)活动2跟踪训练1.随意转动图中两转盘上的指针,指针静止在如图所示的情形时(即蓝色和绿色相配)的概率为(A)A.B.C.D.2.如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是(B)A.B.C.D.第1题图第2题图3.转动如图的转盘两次,两次所指数字之积为奇数,则A胜,偶数则B胜,则A胜的概率为(C)A.B.C.D.4.如图转动两个盘当指针分别指向红色和蓝色时称为配紫色成功.如图转动两个盘各一次配紫色成功的概率是(A)A.B.C.D.活动3课堂小结1.一次试验中可能出现的结果是有限多个,各种结果发生的可能性是相等的.通常可用列表法和树形图法求得各种可能结果.2.一次试验中涉及3个或更多个因素时,不重不漏地求出所有可能的结果,通常采用树形图法.请使用《名校课堂》相应的练习部分