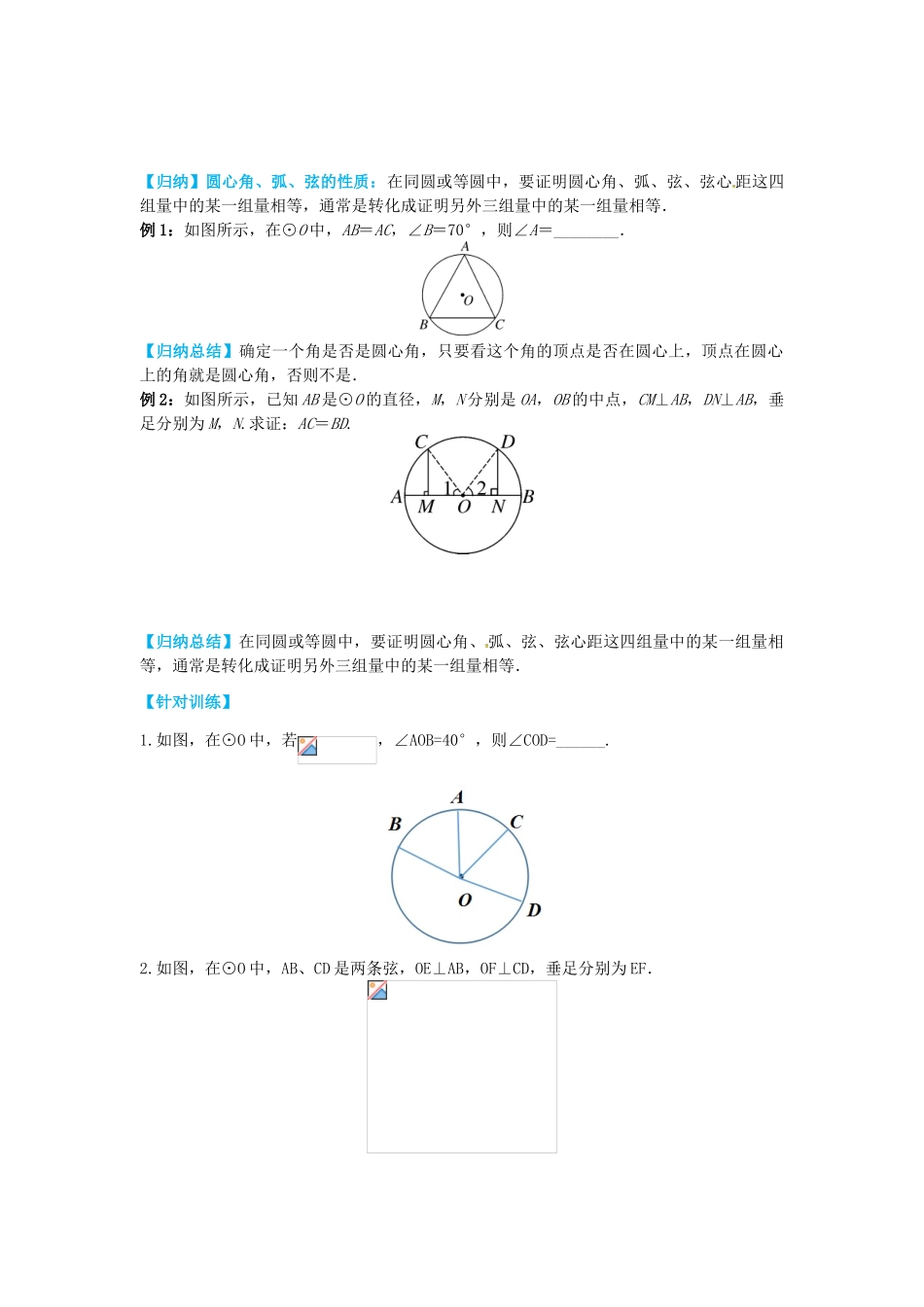
28.3圆心角和圆周角第1课时圆心角学习目标:1.理解并掌握圆心角的定义,能够运用其进行计算.2.理解并掌握圆心角、弧、弦间的关系.学习重点:圆心角、弧、弦间的关系.学习难点:圆心角的定义及其计算.一、知识链接1.圆上任意两点间的线段叫做这个圆的一条____.2.圆上任意的两点间的部分叫做____,简称____,圆的直径将这个圆分成能够完全重合的两条弧,这样的一条弧叫做____;大于半圆的弧叫做____,小于半圆的弧叫做____.二、新知预习2.如图,点A,B在圆O.观察下列各图中的角,总结它们的特点.【概念学习】顶点在圆心的角作圆心角.图____和图_____的角是圆心角.3.每个圆心角对应一条弦和一条弧,圆心角越大,对应的弦越____,对应的圆心角越______.4.猜想:若圆心角相等,所对应的弦、弧有什么关系?三、自学自测1.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD的关系是()A.AB=2CDB.AB>2CDC.AB<2CDD.不能确定四、我的疑惑_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________自主学习一、要点探究探究点1:圆心角的定义问题1:如图所示的圆中,下列各角是圆心角的是()A.∠ABCB.∠AOBC.∠OABD.∠OCB【归纳总结】确定一个角是否是圆心角,只要看这个角的顶点是否在圆心上,顶点在圆心上的角就是圆心角,否则不是.【针对训练】下列说法中正确的是()①圆心角是顶点在圆心的角;、②两个圆心角相等,它们所对的弦也相等;③两条弦相等,圆心到这两条弦的距离相等;④在等圆中,圆心角不等,所对的弦也不等.A.①③B.②④C.①④D.②③探究点2:圆心角、弧、弦间的关系【问题1】如图所示,已知△OAB,将△OAB绕点O顺时针旋转100°得到△ODC.(1)则AB_____CD,∠AOB____∠COD,.(2)若旋转30°,60°,90°,180°,以上结论仍成立吗?【归纳】【做一做】下面的说法正确吗?若不正确,指出错误的原因.(1)如图1,小雨说:“因为弧AB和弧A′B′所对的圆心角都是∠O,所以有弧AB=弧A′B′.”(2)如图2,小华说:“因为AB=CD,所以AB所对的弧AB等于CD所对的弧CD.”【问题2】在同圆或等圆中,若两条弧(或弦)相等,则它们所对的圆心角是否相等,所对的弦(或弧)是否相等?试说明理由.合作探究【归纳】圆心角、弧、弦的性质:在同圆或等圆中,要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等,通常是转化成证明另外三组量中的某一组量相等.例1:如图所示,在⊙O中,AB=AC,∠B=70°,则∠A=________.【归纳总结】确定一个角是否是圆心角,只要看这个角的顶点是否在圆心上,顶点在圆心上的角就是圆心角,否则不是.例2:如图所示,已知AB是⊙O的直径,M,N分别是OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.求证:AC=BD.【归纳总结】在同圆或等圆中,要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等,通常是转化成证明另外三组量中的某一组量相等.【针对训练】1.如图,在⊙O中,若,∠AOB=40°,则∠COD=______.2.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF.(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?(2)如果OE=OF,那么与的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?二、课堂小结内容运用策略弧,弦,圆心角之间的关系在同圆或等圆中,相等的圆心角所对的弦_______,所对的弧也________.①弧,弦,圆心角之间的关系可以证明同圆或等圆中弧相等,角相等以及线段相等;②在应用弧,弦,圆心角之间的关系解决问题时,一定要注意“在同圆或等圆中”这个前提,否则结论不一定成立.弧,弦,圆心角之间的关系的推广同圆或等圆中,两个圆心角,两条弧中有一组量相等,它们所对应的其余各组量也相等1.如图,已知:AB是⊙O的直径,C、D是BE的三等分点,...