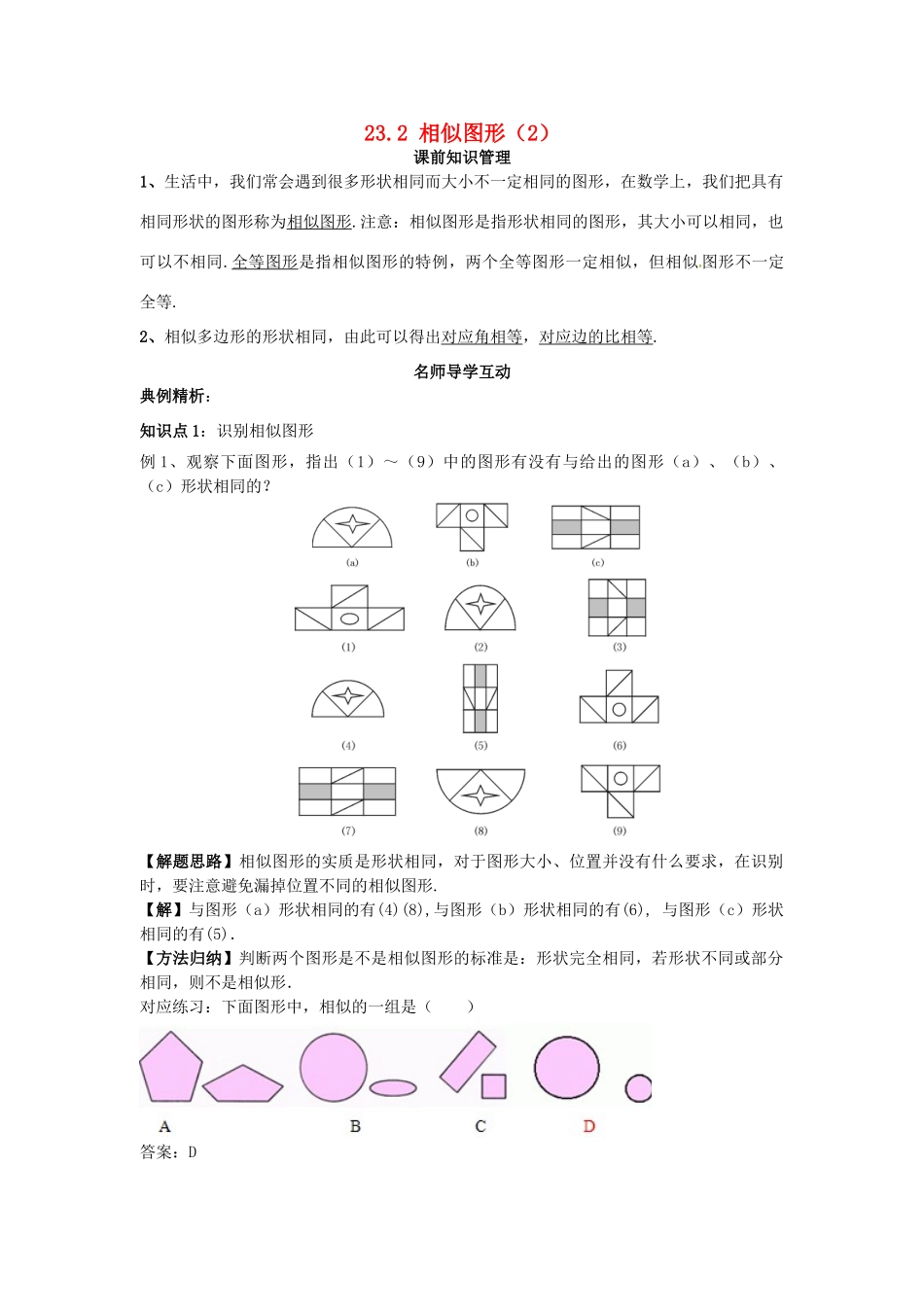
23.2相似图形(2)课前知识管理1、生活中,我们常会遇到很多形状相同而大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似图形.注意:相似图形是指形状相同的图形,其大小可以相同,也可以不相同.全等图形是指相似图形的特例,两个全等图形一定相似,但相似图形不一定全等.2、相似多边形的形状相同,由此可以得出对应角相等,对应边的比相等.名师导学互动典例精析:知识点1:识别相似图形例1、观察下面图形,指出(1)~(9)中的图形有没有与给出的图形(a)、(b)、(c)形状相同的?【解题思路】相似图形的实质是形状相同,对于图形大小、位置并没有什么要求,在识别时,要注意避免漏掉位置不同的相似图形.【解】与图形(a)形状相同的有(4)(8),与图形(b)形状相同的有(6),与图形(c)形状相同的有(5).【方法归纳】判断两个图形是不是相似图形的标准是:形状完全相同,若形状不同或部分相同,则不是相似形.对应练习:下面图形中,相似的一组是()答案:D知识点2:相似多边形例2、如图,四边形ABCD~四边形A′B′C′D′,AB=12,A′B′=6,C′D′=4,∠C=78°,求CD的长及∠C′的度数.【解题思路】相似多边形的对应角相等,对应边成比例.所以,,∠C=∠C′.【解】因为四边形ABCD~四边形A′B′C′D′,所以由相似多边形对应边成比例,得即,∴CD=8.由相似多边形对应角相等,得∠C=∠C′=78°.【方法归纳】解题的关键是要分清它们的对应边及对应角.对应练习:已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于()A、50°B、95°C、35°D、25°答案:C知识点3:图形的放大与缩小例3、把△ABC放大一倍(要求放大后的顶点在格点上).【解题思路】把△ABC放大一倍,可以利用网格将对应的边长扩大成原来的2倍.【解】如图.【方法归纳】图形的放大或缩小,指的是边长的放大或缩小,角是不变的,此时图形的大小发生了变化,但形状不变,即放大或缩小前后的两个图形形状相同,这种由放大或缩小得到的图形与原来的图形相似.在网格中放大或缩小图形时,先确定对应点,再连线.对应练习:请在如图所示的直角坐标系中,画一个五边形.(1)写出它的五个顶点的坐标,然后画出这个五边形关于原点成中心对称的对称图形,并写出对称图形的顶点的坐标;(2)关于原点成中心对称的两个五边形是否全等?是否相似?为什么?答案:(1)图略,五边形ABCDE的各顶点的坐标为A(-3,0),B(-4,-2),C(-3,-4),D(-1,-3),E(0,-1).关于原点成中心对称的五边形A′B′C′D′E′的各顶点的坐标为A′(3,0),B′(4,2),C′(3,4),D′(1,3),E′(0,1).(2)根据对称性知,两个图形的大小、形状不变,这样的两个图形全等.全等图形也是相似图形.易错警示1、忽视图形放大或缩小时角的大小不变例4、在5倍放大镜下观看一个20°的角,所看到的角的度数是多少?错解:5×20°=100°,所以在5倍放大镜下看一个20°的角,所看到的角的度数是100°.错因分析:在放大镜下观看一个角,其大小不变,原来的角是多少度,不论放大镜放大的倍数是多少,所看到的角的度数与原来一样.正解:20°.角的度数只取决于角的两边张开的大小.例5、如图,矩形ABCD的四周加宽1个单位,所得到的矩形EFGH与原来的矩形ABCD相似吗?错解:相似.错因分析:矩形EFGH初看似乎是由矩形ABCD放大而得到的,但事实上由于矩形ABCD的长和宽不一样,放大某个倍数后,长和宽增加的长度也就不一样,而图中长和宽增加的长度却是相同的.正解:矩形EFGH和ABCD不相似,只有当AB=BC时,二者才相似.课堂练习评测知识点1:判断图形是否相似1、在下列四组图形中,不相似的有()A.1组B.2组C.3组D.4组2、下列图形中是____与_____相似的.知识点2:相似比3、如图,有两个形状相同的星星图案,则x的值为()A.15B.12C.10D.8知识点3:画相似图形4、下列图形分别分成四小块,使它们的形状、大小完全相同,并且与原图相似,应怎样分?(画出大致图形即可)课后作业练习基础训练1、下面给出的图形中,不是相似图形的是()A.刚买的一双手套的左右两只B.仅仅宽度不同的两快长方形木板C.一对羽毛球球拍D.复印出...