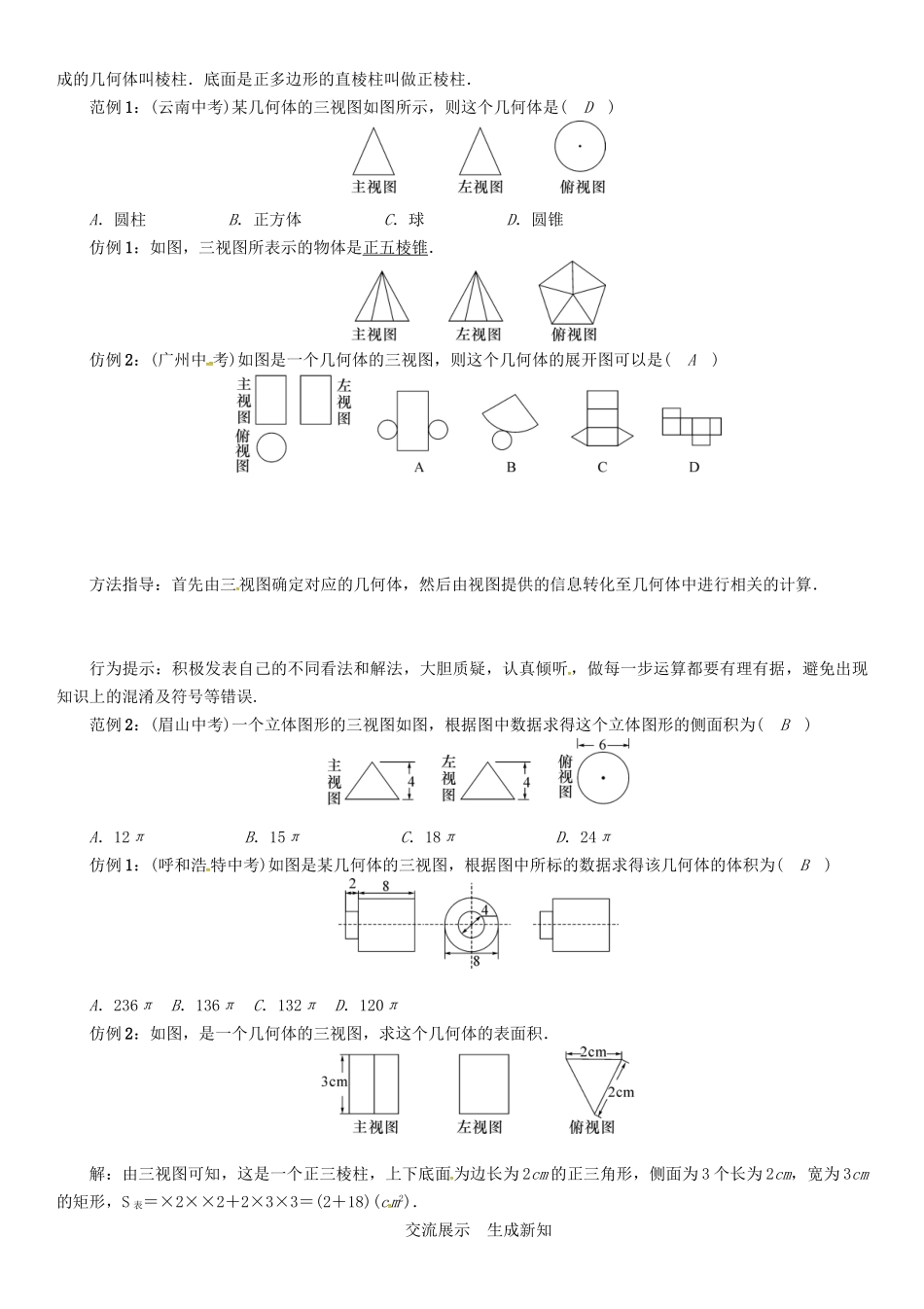
课题:由三视图确定几何体及计算【学习目标】1.学会根据物体的三视图描述出几何体的基本形状或实物原型;2.经历探索简单的几何体的三视图的还原,进一步发展空间想象能力.【学习重点】根据物体的三视图描述出几何体的基本形状或实物原型.【学习难点】注重立体图形的构成.行为提示:创景设疑,帮助学生知道本节课学什么.行为提示:认真阅读课本,独立完成“自学互研”中的题目,并在练习中发现规律,从猜测到探索到理解知识.方法指导:由物体的三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合想象出整体形状.情景导入生成问题旧知回顾:什么是几何体的三视图?答:自几何体的前方向后投射,在正投影面上得到的视图称为主视图;自几何体的上方向下投射,在水平投影面上得到的视图称为俯视图;自几何体的左侧向右投射,在侧投影面上得到的视图称为左视图.上述三种视图统称为一个物体的三视图.自学互研生成能力阅读教材P82~P83,完成以下问题:1.主视图、俯视图、左视图,分别反映几何体的什么?答:主视图反映的是几何体的长和高;俯视图反映的是几何体的长和宽;左视图反映的是几何体的宽和高.2.什么是棱柱?正棱柱?答:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫棱柱.底面是正多边形的直棱柱叫做正棱柱.范例1:(云南中考)某几何体的三视图如图所示,则这个几何体是(D)A.圆柱B.正方体C.球D.圆锥仿例1:如图,三视图所表示的物体是正五棱锥.仿例2:(广州中考)如图是一个几何体的三视图,则这个几何体的展开图可以是(A)方法指导:首先由三视图确定对应的几何体,然后由视图提供的信息转化至几何体中进行相关的计算.行为提示:积极发表自己的不同看法和解法,大胆质疑,认真倾听,做每一步运算都要有理有据,避免出现知识上的混淆及符号等错误.范例2:(眉山中考)一个立体图形的三视图如图,根据图中数据求得这个立体图形的侧面积为(B)A.12πB.15πC.18πD.24π仿例1:(呼和浩特中考)如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为(B)A.236πB.136πC.132πD.120π仿例2:如图,是一个几何体的三视图,求这个几何体的表面积.解:由三视图可知,这是一个正三棱柱,上下底面为边长为2cm的正三角形,侧面为3个长为2cm,宽为3cm的矩形,S表=×2××2+2×3×3=(2+18)(cm2).交流展示生成新知1.将阅读教材时生成的新问题和通过“自学互研”得出的结论展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一由三视图确定几何体知识模块二根据三视图进行相关计算检测反馈达成目标【当堂检测】见所赠光盘和学生用书;【课后检测】见学生用书.课后反思查漏补缺1.收获:__________________________________________________________________2.存在困惑:_____________________________________________________________