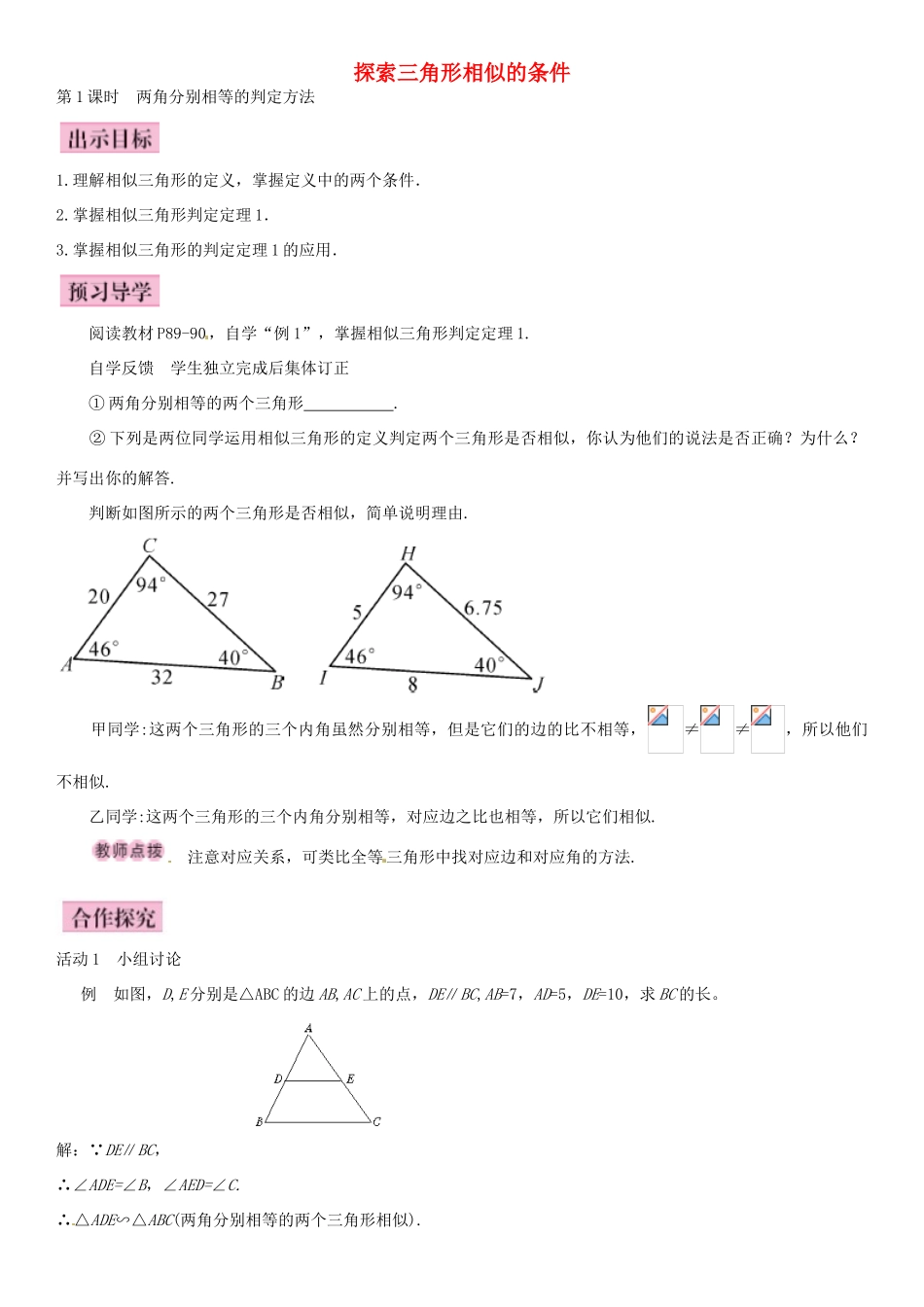
探索三角形相似的条件第1课时两角分别相等的判定方法1.理解相似三角形的定义,掌握定义中的两个条件.2.掌握相似三角形判定定理1.3.掌握相似三角形的判定定理1的应用.阅读教材P89-90,自学“例1”,掌握相似三角形判定定理1.自学反馈学生独立完成后集体订正①两角分别相等的两个三角形.②下列是两位同学运用相似三角形的定义判定两个三角形是否相似,你认为他们的说法是否正确?为什么?并写出你的解答.判断如图所示的两个三角形是否相似,简单说明理由.甲同学:这两个三角形的三个内角虽然分别相等,但是它们的边的比不相等,≠≠,所以他们不相似.乙同学:这两个三角形的三个内角分别相等,对应边之比也相等,所以它们相似.注意对应关系,可类比全等三角形中找对应边和对应角的方法.活动1小组讨论例如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长。解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC(两角分别相等的两个三角形相似).∴=.∴BC===14.运用相似三角形可以进行边的计算.活动2跟踪训练(独立完成后展示学习成果)1.下面能够相似的一组三角形为()A.两个等腰三角形B.两个直角三角形C.两个等边三角形D.以上都不对2.如图,AB∥CD∥EF,则图中相似三角形有()A.4对B.3对C.2对D.1对第2题图第3题图第4题图3.如图,∠AED=∠B,一定可得()A.AD:AC=AE:ABB.DE:BC=AD:DBC.DE:BC=AE:ACD.AD:AB=AE:AC4.如图,已知∠1=∠2=∠3,则下列表达式正确的是()A.B.C.D.5.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形(用相似符号连接).DEFCBA按照一定的顺序去寻找相似三角形.6.如图,,,,,则.7.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=.第7题图第8题图8.在平行四边形ABCD中,E在DC上,若DE:EC=1:2,则BF:BE=.9.如图,若,那么与相似吗?吗?为什么?活动3课堂小结学生试述:这节课你学到了些什么?【预习导学2】自学反馈①相似②略【合作探究2】活动2跟踪训练1.C2.B3.A4.C5.△BDE∽△CDF,△ABF∽△ACE6.7.48.3:59.∵.,又,∴.∴.∴.