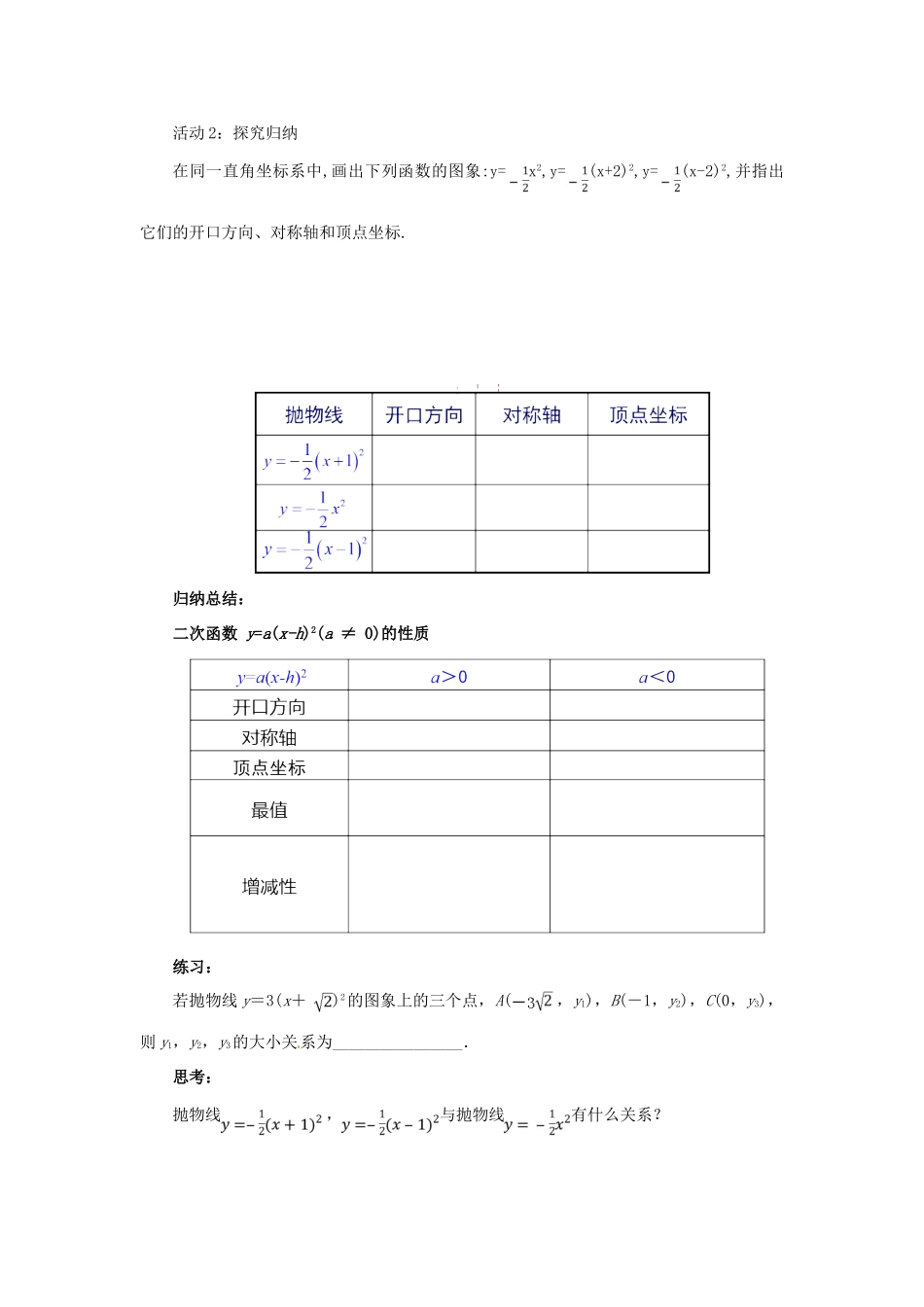
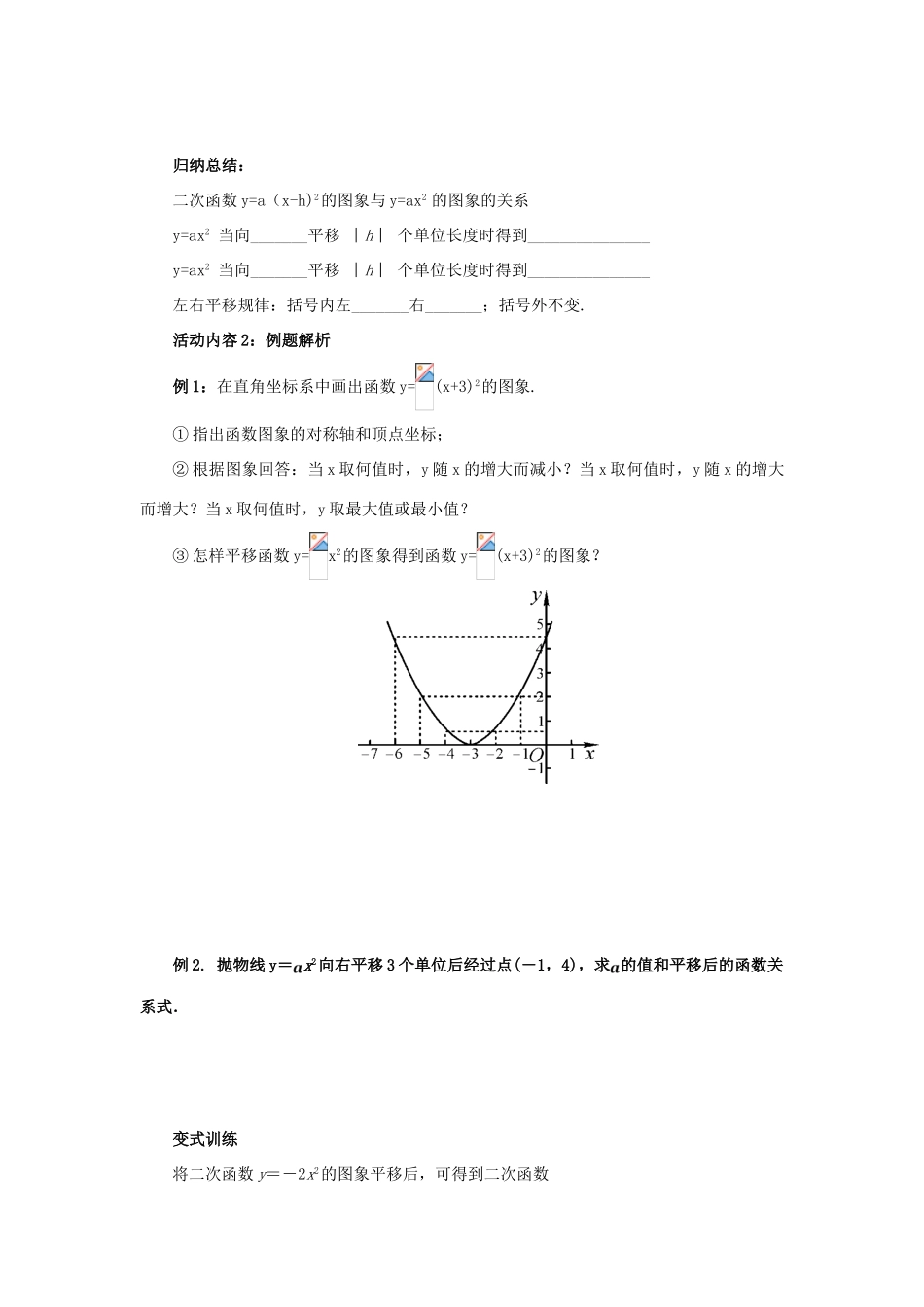
22.1.3二次函数y=a(x-h)²的图象和性质第2课时一、学习目标:1、会画二次函数y=a(x-h)2的图象;2、掌握二次函数y=a(x-h)2的性质并会应用;3、理解y=ax2与y=a(x-h)2之间的联系.二、学习重难点:重点:会画二次函数y=a(x-h)2的图象;难点:掌握二次函数y=a(x-h)2的性质并会应用.探究案三、教学过程(一)复习巩固说说二次函数y=ax2+c(a≠0)的图象的特征.活动内容1:活动1:小组合作情景问题:问题1二次函数y=ax2+k(a≠0)与y=ax2(a≠0)的图象有何关系?问题2函数的图象,能否也可以由函数平移得到?活动2:探究归纳在同一直角坐标系中,画出下列函数的图象:y=x2,y=(x+2)2,y=(x-2)2,并指出它们的开口方向、对称轴和顶点坐标.归纳总结:二次函数y=a(x-h)2(a≠0)的性质练习:若抛物线y=3(x+)2的图象上的三个点,A(,y1),B(-1,y2),C(0,y3),则y1,y2,y3的大小关系为________________.思考:抛物线,与抛物线有什么关系?归纳总结:二次函数y=a(x-h)2的图象与y=ax2的图象的关系y=ax2当向_______平移︱h︱个单位长度时得到_______________y=ax2当向_______平移︱h︱个单位长度时得到_______________左右平移规律:括号内左_______右_______;括号外不变.活动内容2:例题解析例1:在直角坐标系中画出函数y=(x+3)2的图象.①指出函数图象的对称轴和顶点坐标;②根据图象回答:当x取何值时,y随x的增大而减小?当x取何值时,y随x的增大而增大?当x取何值时,y取最大值或最小值?③怎样平移函数y=x2的图象得到函数y=(x+3)2的图象?例2.抛物线y=x2向右平移3个单位后经过点(-1,4),求的值和平移后的函数关系式.变式训练将二次函数y=-2x2的图象平移后,可得到二次函数y=-2(x+1)2的图象,平移的方法是()A.向上平移1个单位B.向下平移1个单位C.向左平移1个单位D.向右平移1个单位随堂检测1.把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是.2.二次函数y=2(x-)2图象的对称轴是直线____,顶点是________.3.若(-,y1)(-,y2)(,y3)为二次函数y=(x-2)2图象上的三点,则y1,y2,y3的大小关系为_______________.4.若抛物线y=a(x-h)²的顶点是(-3,0),它是由抛物线y=-2x²通过平移而得到的,则a=_______,h=_______.5.指出下列函数图象的开口方向,对称轴和顶点坐标.6.在同一坐标系中,画出函数y=2x2与y=2(x-2)2的图象,分别指出两个图象之间的相互关系.课堂小结通过本节课的学习在小组内谈一谈你的收获,并记录下来:我的收获______________________________________________________________________________________________________________________________________________________参考答案复习巩固问题1当k>0时二次函数y=ax2+k(a≠0)是由y=ax2(a≠0)的图象向上平移k个单位长度当k<0时二次函数y=ax2+k(a≠0)是由y=ax2(a≠0)的图象向下平移|k|个单位长度问题2函数的图象是由函数向右平移2个单位长度得到归纳总结:练习:y2<y3<y1思考:抛物线向左平移1个单位得到抛物线;抛物线向右平移1个单位得到抛物线归纳总结:右y=a(x-h)2左y=a(x+h)2加减例题解析例1解:①对称轴是直线x=-3,顶点坐标为(-3,0);②当x<-3时,y随x的增大而减小;当x>-3时,y随x的的增大而增大;当x=-3时,y有最小值.③将函数的图象沿x轴向左平移3个单位得到函数的图象.例2解:二次函数y=x2的图象向右平移3个单位后的二次函数关系式可表示为y=(x-3)2,把x=-1,y=4代入,得4=(-1-3)2,,∴平移后二次函数关系式为y=(x-3)2.变式训练:C随堂检测1.y=-(x+3)2或y=-(x-3)22.,3.y1〉y2〉y34.-2-35.6.解:图象如图.函数y=2(x-2)2的图象由函数y=2x2的图象向右平移2个单位得到.