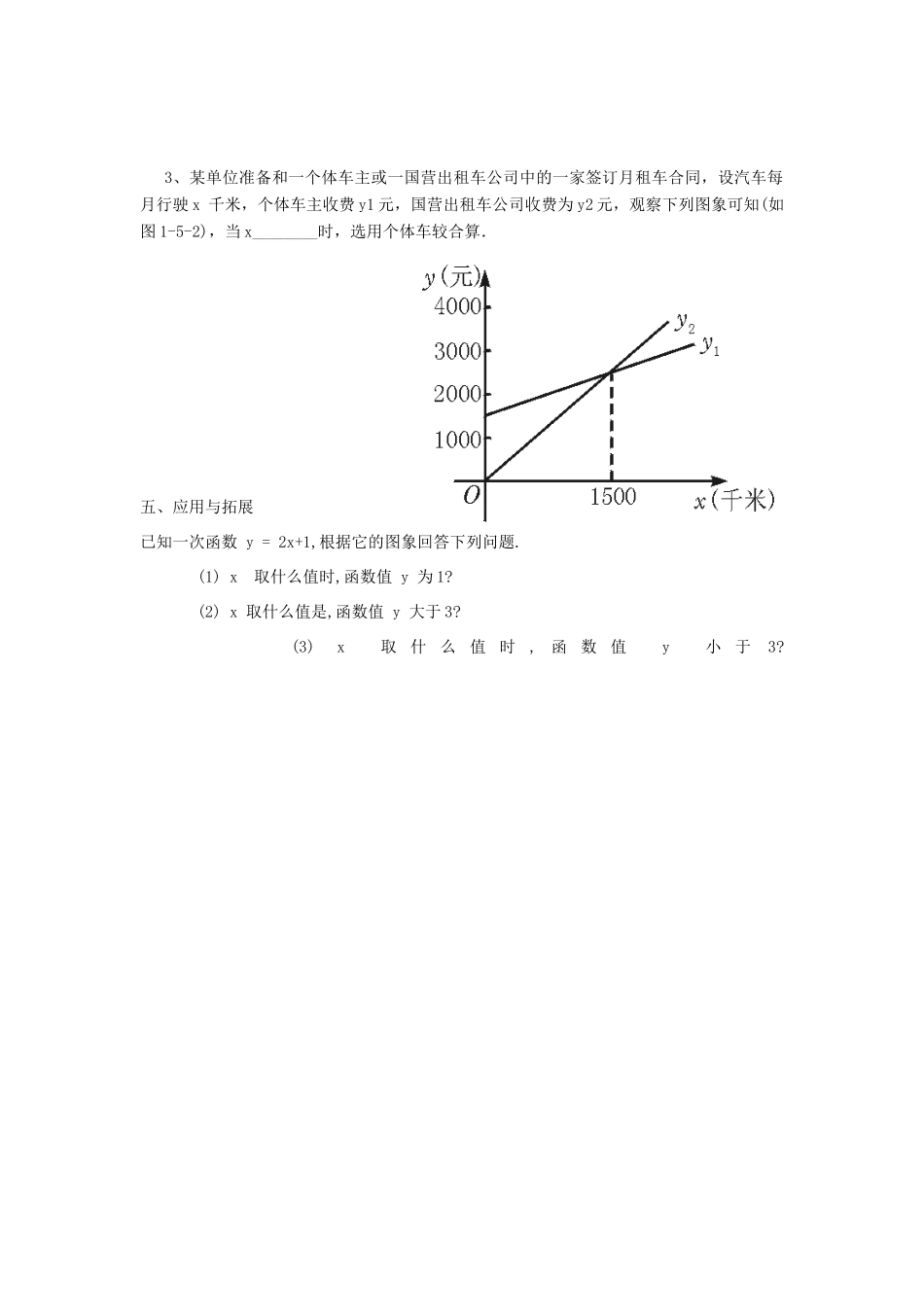
14.3.2一次函数与一元一次不等式教学目标(一)教学知识点1.认识一元一次不等式与一次函数问题的转化关系.2.学会用图象法求解不等式.3.进一步理解数形结合思想.(二)能力训练要求1.培养提高从不同方向思考问题的能力.2.探究解题思路,以便灵活运用知识.3.提高问题间互相转化的技能.(三)情感与价值观要求1.积极参与活动,培养学习兴趣.2.形成合作交流的意识及独立思考的习惯.教学重点1.理解一元一次不等式与一次函数的转化关系及本质联系.2.掌握用图象求解不等式的方法.教学难点图象法求解不等式中自变量取值范围的确定.一、学前准备二、探究学习:(一)自主探究我们先观察函数y=2x-4的图象.可以看出:当x时,直线y=2x-4上的点全在x轴上方,即这时y=2x-40.(填<或>)由此可知,通过函数图象也可求得不等式的解为x>2.(二)合作探究三、回顾、思考1、请你对本节课所学知识作个小结,你有哪些收获?2、预习时的疑惑解决了吗?还有哪些疑惑?3、你认为老师上课时还有哪些需要注意的地方?四、自我测试1.当自变量x的取值满足什么条件时,函数y=3x+8的值满足下列条件?(1)y=-7.(2)y>0(3)y<2.(4)y>-12.利用图象解出x:6x-4<3x+2.3、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知(如图1-5-2),当x________时,选用个体车较合算.五、应用与拓展已知一次函数y=2x+1,根据它的图象回答下列问题.(1)x取什么值时,函数值y为1?(2)x取什么值是,函数值y大于3?(3)x取什么值时,函数值y小于3?六、我反思,我进步七、作业批改记录: