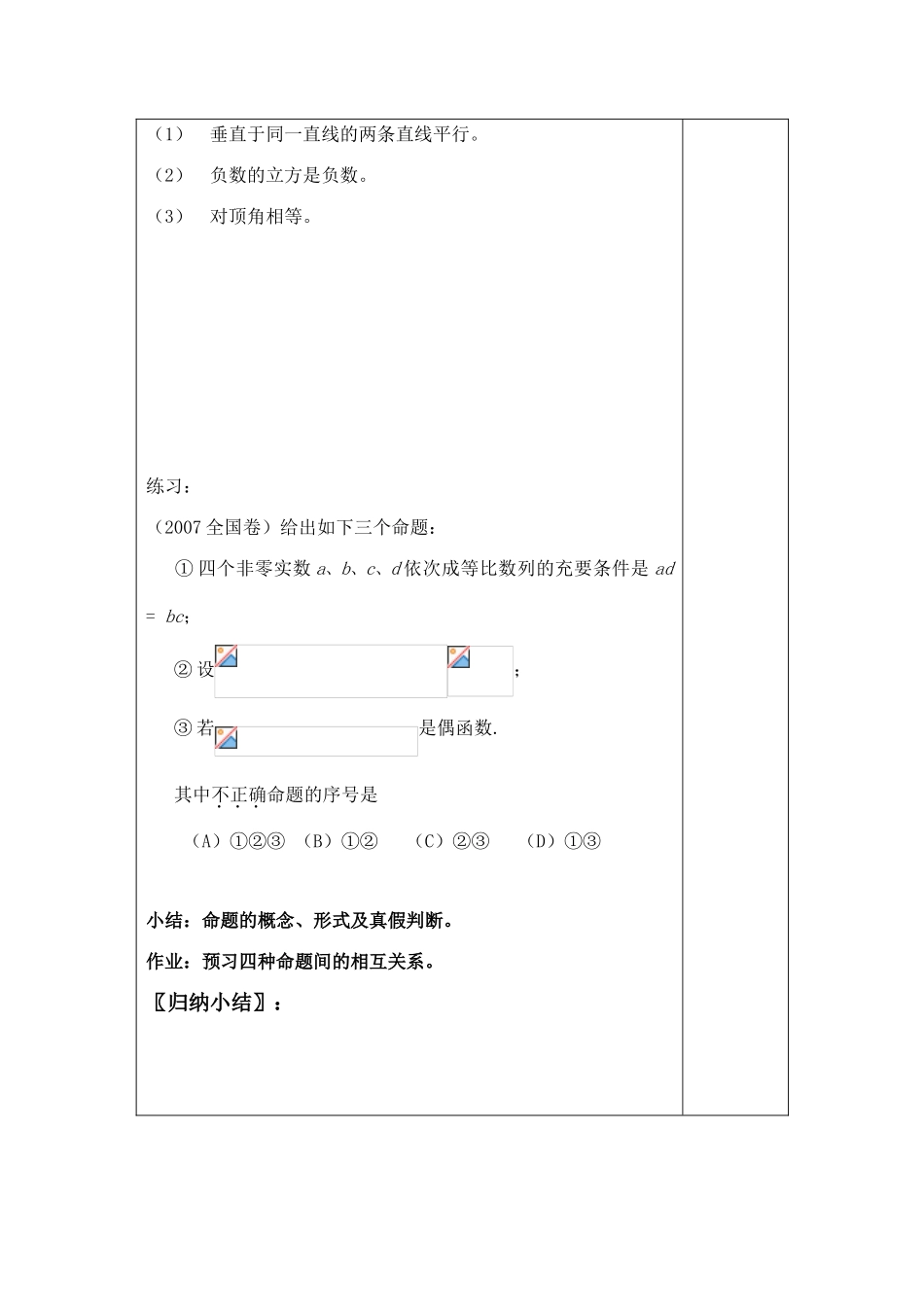
命题讲学案〖学习目标及要求〗:1、学习目标:(1)、命题的概念(2)、命题的形式(3)、命题的真假判断2、重点难点:命题的形式及真假判断3、高考要求:掌握命题形式,理解真假判断〖讲学过程〗:探究一:判断下列语句哪些是命题?是真命题还是假命题?(1)空集是任何集合的子集。(2)若整数a是素数,则a是奇数。(3)指数函数是增函数吗?(4)若空间中两条直线不相交,则这两条直线平行。(5)(6)探究二:指出下列命题中的条件p和结论q。(1)若整数a能被2整除,则a是偶数。(2)若四边形是菱形,则它的对角线互相垂直且平分。(3)垂直于同一直线的两个平面平行。探究三:将下列命题改写成“若p,则q”的形式,并判断真假:感悟一:感悟二:感悟三(1)垂直于同一直线的两条直线平行。(2)负数的立方是负数。(3)对顶角相等。练习:(2007全国卷)给出如下三个命题:①四个非零实数a、b、c、d依次成等比数列的充要条件是ad=bc;②设;③若是偶函数.其中不正确命题的序号是(A)①②③(B)①②(C)②③(D)①③小结:命题的概念、形式及真假判断。作业:预习四种命题间的相互关系。〖归纳小结〗: