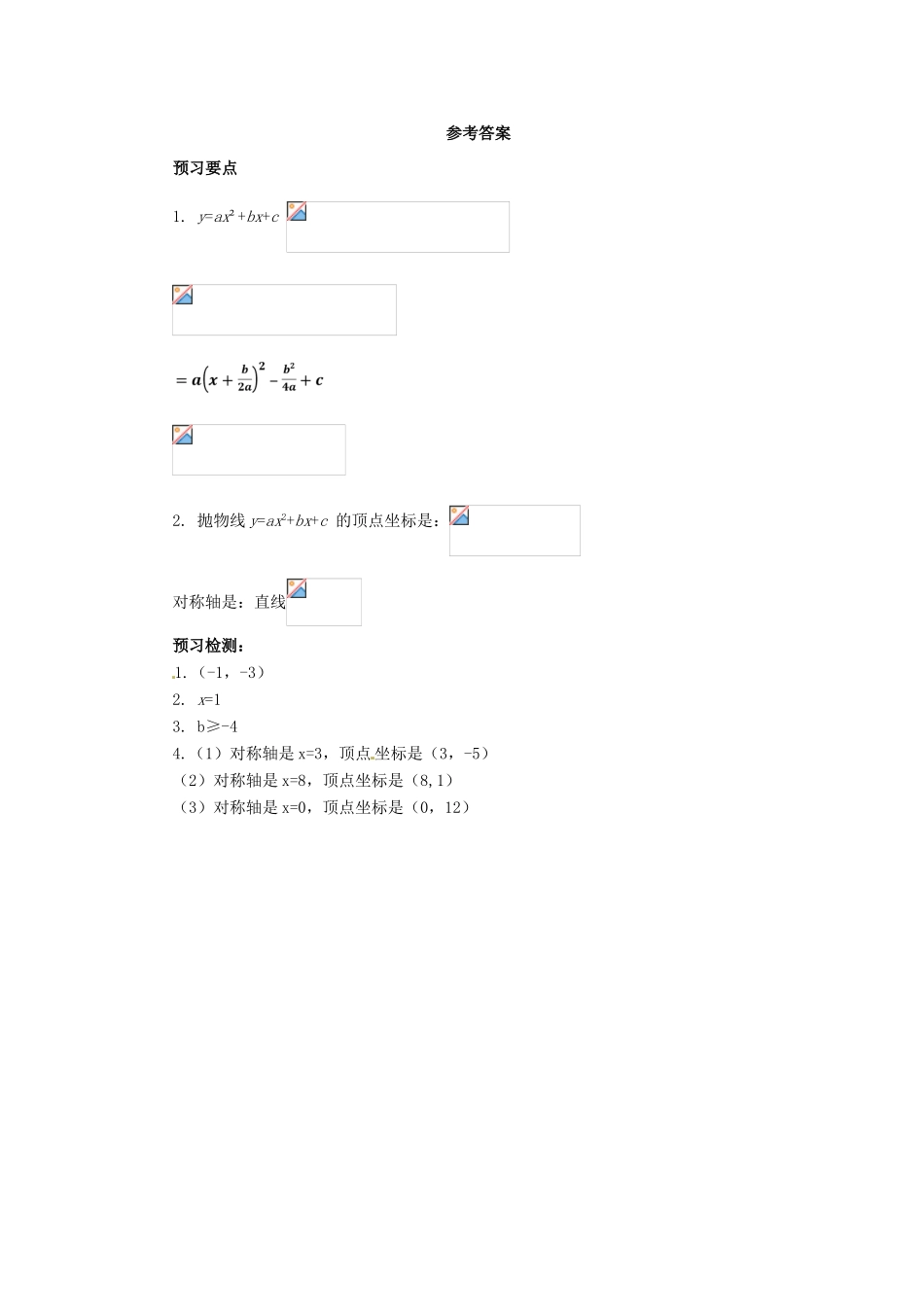
22.1.4二次函数y=ax2+bx+c的图象和性质第1课时一、预习目标及范围:1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.3.预习范围:37——39页,并完成课后练习二、预习要点1.用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.2.写出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.三、预习检测1、二次函数y=2(x+1)2-3的顶点坐标是。2、抛物线y=x2-2x-1的对称轴为。3、已知二次函数y=x2+bx+3,其中b为常数,当x≥2时,函数值y随着x的增大而增大,则b的取值范围是.4、根据公式确定下列二次函数图象的对称轴和顶点坐标:我的疑惑在预习过程中的存在哪些困惑与建议填写在下面,并与同学交流。__________________________________________________________________________________________________________________________________________________________参考答案预习要点1.y=ax²+bx+c2.抛物线y=ax2+bx+c的顶点坐标是:对称轴是:直线预习检测:1.(-1,-3)2.x=13.b≥-44.(1)对称轴是x=3,顶点坐标是(3,-5)(2)对称轴是x=8,顶点坐标是(8,1)(3)对称轴是x=0,顶点坐标是(0,12)