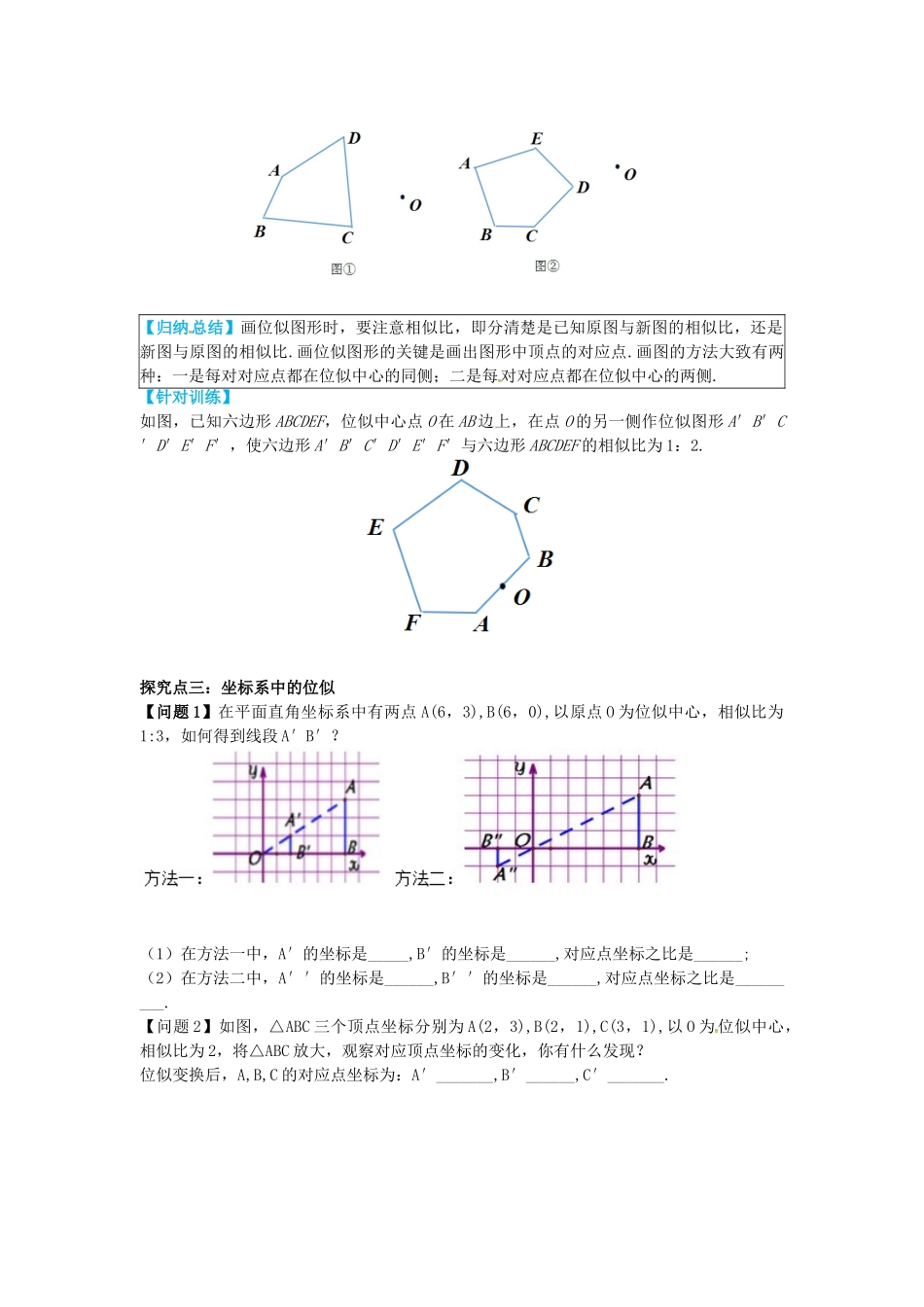
25.7相似多边形和图形的位似第2课时位似图形学习目标:1.理解并掌握位似图形的相关概念.2..学习并掌握位似图形的性质并能够运用其解决问题.学习重点:位似图形的性质.学习难点:运用位似图形的性质解决问题.一、知识链接1.已知△ABC,请作一个△A'B'C',使它们的相似比为1:2.二、新知预习2.如图,是日常生活中常见的一些图形.请观察,图中有相似图形吗?如果有,这种相似有什么特征?3.如图,点O在四边形ABCD的内部,在其外部作一个四边形A'B'C'D',使得四边形ABCD∽四边形A'B'C'D',且相似比为1:2.,请仿照作法作出另一个相似比为1:3的四边形A''B''C''D'',观察这两个图形有何特点.【归纳】像这样的图形,它们不仅相似,而且经过每对对应点的直线______,对应边互相____行(或在_______).我们把这样的图形称为位似图形.自主学习三、自学自测.观察下图中的多边形,判断它们是不是位似图形,再经过计算后验证你的结论.四、我的疑惑_________________________________________________________________________________________________________________________________________________________________________________________________一、要点探究探究点1:位似图形的概念及性质例1:如图所示,指出下列各图中两个图形是否是位似图形?若是,请指出位似中心.【归纳总结】解决此类题的关键是首先要判断两个图形是不是相似图形,然后再找出对应点,作出几对对应点所在的直线,观察是否经过同一个点.若两个图形是相似图形,且所作的直线经过同一个点,则这两个图形是位似图形.【针对训练】下面说法:(1)相似图形一定是位似图形(2)位似图形一定是相似的图形(3)同一底片时底片上的图形和银幕上的图形是位似图形,其中正确的说法有()A、1个B、2个C、3个D、4个探究点2:位似图形的画法例2:(1)如图①,在位似中心点O的异侧,作出已知四边形ABCD的位似图形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD的相似比为2:3;(2)如图②,已知五边形ABCDE,在位似中心点O的同侧作五边形ABCDE的位似图形A′B′C′D′E′,使五边形A′B′C′D′E′与五边形ABCDE的相似比为1:3;合作探究【归纳总结】画位似图形时,要注意相似比,即分清楚是已知原图与新图的相似比,还是新图与原图的相似比.画位似图形的关键是画出图形中顶点的对应点.画图的方法大致有两种:一是每对对应点都在位似中心的同侧;二是每对对应点都在位似中心的两侧.【针对训练】如图,已知六边形ABCDEF,位似中心点O在AB边上,在点O的另一侧作位似图形A′B′C′D′E′F′,使六边形A′B′C′D′E′F′与六边形ABCDEF的相似比为1:2.探究点三:坐标系中的位似【问题1】在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,如何得到线段A′B′?(1)在方法一中,A′的坐标是_____,B′的坐标是______,对应点坐标之比是______;(2)在方法二中,A′′的坐标是______,B′′的坐标是______,对应点坐标之比是_________.【问题2】如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(3,1),以O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?位似变换后,A,B,C的对应点坐标为:A′_______,B′______,C′_______.【归纳】在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于__________.例3:如图,在平面直角坐标系中,A(1,2),B(2,4),C(4,5),D(3,1)围成四边形ABCD,作出一个四边形ABCD的位似图形,使得新图形与原图形对应线段的比为2:1,位似中心是坐标原点.【归纳总结】画以原点为位似中心的位似图形的方法:将一个多边形各点的横坐标与纵坐标都乘±k(或除以±k),可得新多边形各顶点的坐标,描出这些点并顺次连接这些点即可.【针对训练】在平面直角坐标系中,已知点A(6,4),B(4,-2),以原点O为位似中心,相似比为把△ABO缩小,则点A的对应点A′的坐标是()A.(3,2)B.(12,8)C.(12,8)或(-12,-8)D.(3,2)或(-3,-2)二、课堂小结内容基本图形概念它们不仅相似,而且经过每对...