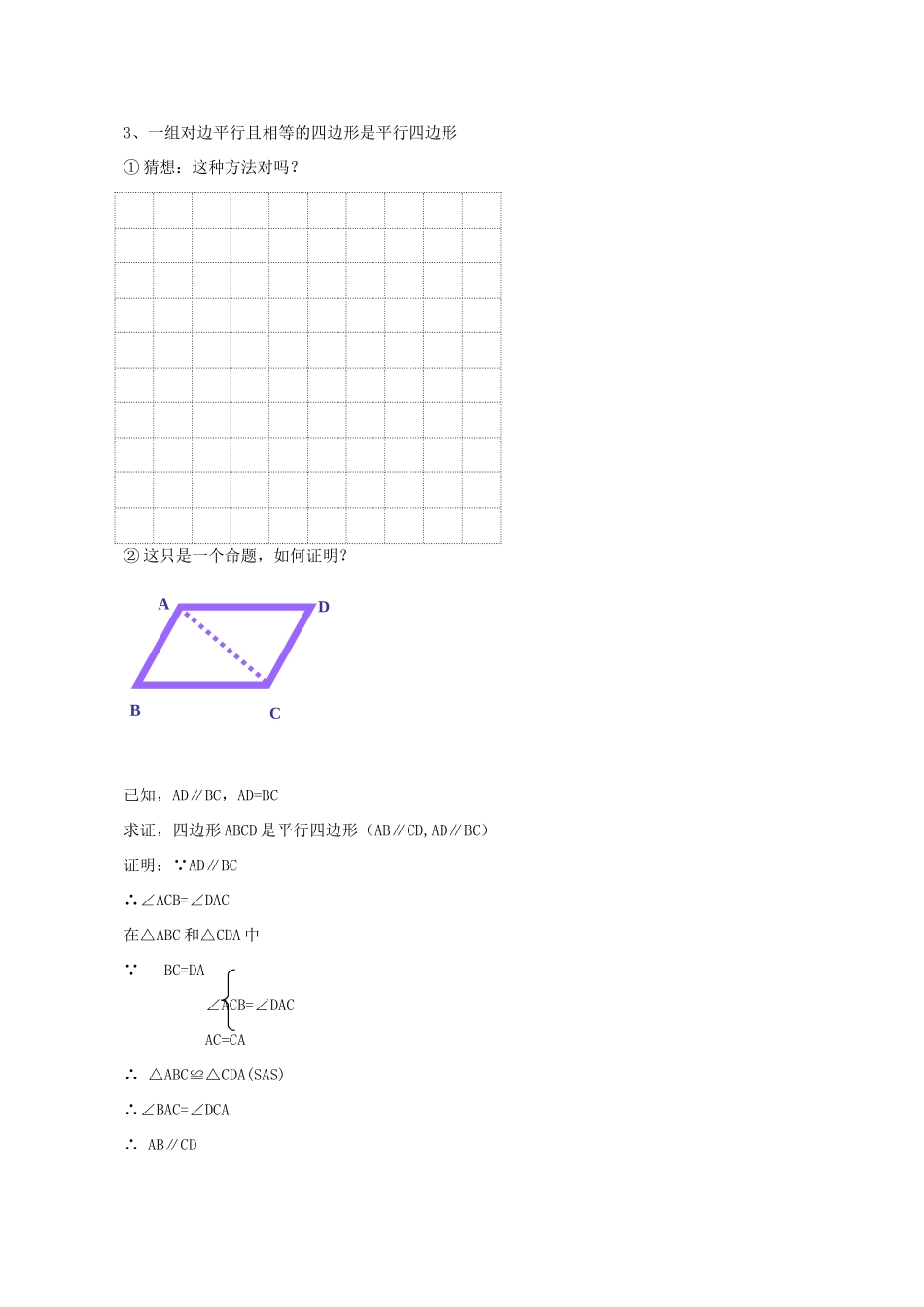
平行四边形的性质[一、创设情境,引入课题]1、复习旧知,奠定基础(学生课前填写学案)①研究三角形从哪两个方面研究?三角形全等的判定方法。②平行四边形的定义③平行四边形的性质从哪几个方面去研究?平行四边形有哪些性质?1、边:对边平行且相等(学生回答)平行四边形的性质2、角:对角相等,邻角互补3、对角线:对角线互相平分2、创设情境,引入课题装潢店要招聘店员,老板出了这样一道考题:“在装修过程中你不小心将顾客家中的一块平行四边形的镜子碰碎了,只剩下如图所示部分,现要配一块一模一样的,你能想到什么办法?并说明这张玻璃符合顾客要求的道理。”你能为应聘人员设计一个方案吗?[二、合作学习,探索归纳]小组讨论方案,5min。合作学习要求:1、在方格纸中画图找方案(提示:找性质的逆命题)本节课主要从边的方面研究判定方法2、找出理论依据3、说出平行四边形的判定方法预想提出的方案(挑选不同做法的几个组各推荐一名思路清晰的同学在投影仪下给大家画出图形并讲解)1、两组对边分别平行的四边形是平行四边形(定义)∵AB∥CD,AD∥BC∴四边形ABCD是平行四边形2、两组对边分别相等的四边形是平行四边形①猜想:这种方法对吗?②这只是一个命题,如何证明?已知,AD=BC,AB=CD求证:四边形ABCD是平行四边形(AB∥CD,AD∥BC)证明:在△ABC和△CDA中∵AB=CDBC=DAAC=CA∴△ABC≌△CDA(SSS)∴∠ACB=∠DAC,∠BAC=∠DCA∴AD∥BC,AB∥CD∴四边形ABCD是平行四边形③几何语言如何描述?∵AB=CD,AD=BC∴四边形ABCD是平行四边形DBAC3、一组对边平行且相等的四边形是平行四边形①猜想:这种方法对吗?②这只是一个命题,如何证明?已知,AD∥BC,AD=BC求证,四边形ABCD是平行四边形(AB∥CD,AD∥BC)证明:∵AD∥BC∴∠ACB=∠DAC在△ABC和△CDA中∵BC=DA∠ACB=∠DACAC=CA∴△ABC≌△CDA(SAS)∴∠BAC=∠DCA∴AB∥CDDBAC∵AD∥BC∴四边形ABCD是平行四边形③几何语言如何描述?∵AD∥BC,AD=BC∴四边形ABCD是平行四边形4、……建构知识:判别1、两组对边分别平行的四边形是平行四边形.∵AB∥CD,AC∥BD∴四边形ABCD是平行四边形判别2、两组对边分别相等的四边形是平行四边形∵AB=CD,AD=BC,∴四边形ABCD为平行四边形判别3、一组对边平行且相等的四边形是平行四边形.∵AB=CD,AB∥CD∴四边形ABCD是平行四边形[三、范例赏析]例、如图,在平行四边形ABCD中,E、F分别是AD和BC的中点。求证:四边形BFDE是平行四边形。(同学们各抒己见,找出不同的做法)证明:∵ABCD是平行四边形∴AD∥BC,AD=BC∵E、F分别是AD和BC的中点∴DE=½AD,BF=½BC∴DE=BF∴四边形BFDE是平行四边形[四、夯实基础]1、分别说明下列条件能不能判定四边形是平行四边形,为什么?A、AB∥CD,AD∥BCB、AB=CD,AD=BCC、AB∥CD,AB=CDD、AB∥CD,∠A=∠C(证明)2、如图,四边形ABCD是平行四边形,PQ是对角线BD上的两个点,且BP=DQ求证:AP∥QC,AP=QC[五、当堂达标]如图:平行四边形ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形。你能想出几种方法?你还有其它判定平行四边形的方法吗?CBODAFEADBCPQ