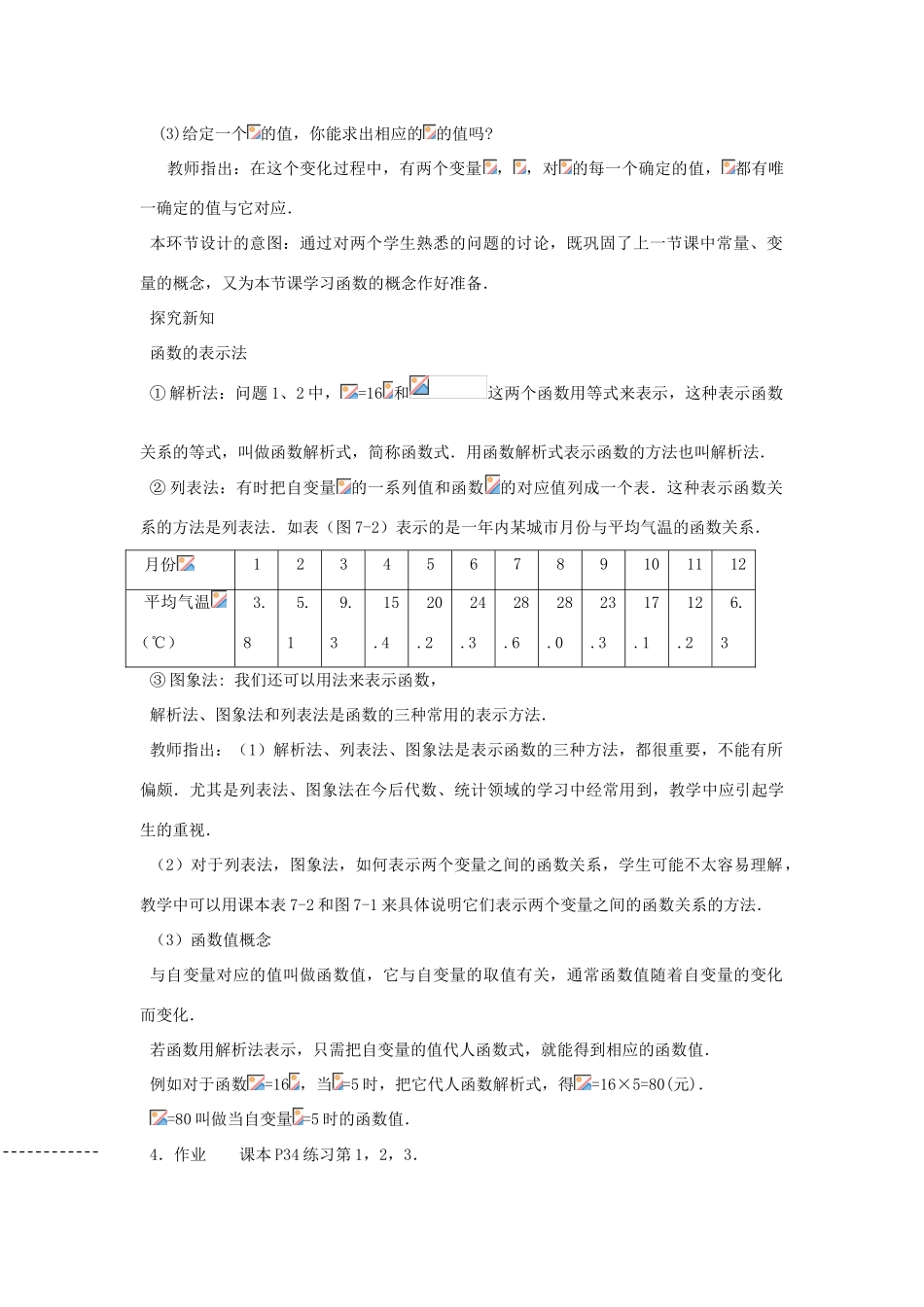
2.1函数和它的表示法(第二课时)〖教学目标〗1、了解函数的三种表示法:(1)解析法;(2)列表法;(3)图象法..2、理解函数值的概念.3、会在简单情况下,根据函数的表示式求函数的值.〖教学重点与难点〗教学重点:函数的表示法,是今后进一步学习其他函数,以及运用函数模型解决实际问题的基础,因此函数的有关概念是本节的重点.教学难点:用图象来表示函数关系涉及数形结合,学生理解它需要一个较长且比较具体的过程,是本节教学的难点.〖教学方法〗观察、比较、合作、交流、探索.〖教学过程〗教学过程分以下6个环节:创设情境问题1小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算.设小明的哥哥这个月工作的时间为时,应得报酬为元,填写下表:工作时间(时)15101520……报酬(元)然后回答下列问题:(1)在上述问题中,哪些是常量?哪些是变量?(常量16,变量、)(2)能用的代数式来表示的值吗?(能,=16)教师指出:在这个变化过程中,有两个变量,,对的每一个确定的值,都有唯一确定的值与它对应.问题2跳远运动员按一定的起跳姿势,其跳远的距离(米)与助跑的速度(米/秒)有关.根据经验,跳远的距离(0<<10.5).然后回答下列问题:(1)在上述问题中,哪些是常量?哪些是变量?(常量0.085,变量、)(2)计算当分别为7.5,8,8.5时,相应的跳远距离是多少(结果保留3个有效数字)?(3)给定一个的值,你能求出相应的的值吗?教师指出:在这个变化过程中,有两个变量,,对的每一个确定的值,都有唯一确定的值与它对应.本环节设计的意图:通过对两个学生熟悉的问题的讨论,既巩固了上一节课中常量、变量的概念,又为本节课学习函数的概念作好准备.探究新知函数的表示法①解析法:问题1、2中,=16和这两个函数用等式来表示,这种表示函数关系的等式,叫做函数解析式,简称函数式.用函数解析式表示函数的方法也叫解析法.②列表法:有时把自变量的一系列值和函数的对应值列成一个表.这种表示函数关系的方法是列表法.如表(图7-2)表示的是一年内某城市月份与平均气温的函数关系.月份123456789101112平均气温(℃)3.85.19.315.420.224.328.628.023.317.112.26.3③图象法:我们还可以用法来表示函数,解析法、图象法和列表法是函数的三种常用的表示方法.教师指出:(1)解析法、列表法、图象法是表示函数的三种方法,都很重要,不能有所偏颇.尤其是列表法、图象法在今后代数、统计领域的学习中经常用到,教学中应引起学生的重视.(2)对于列表法,图象法,如何表示两个变量之间的函数关系,学生可能不太容易理解,教学中可以用课本表7-2和图7-1来具体说明它们表示两个变量之间的函数关系的方法.(3)函数值概念与自变量对应的值叫做函数值,它与自变量的取值有关,通常函数值随着自变量的变化而变化.若函数用解析法表示,只需把自变量的值代人函数式,就能得到相应的函数值.例如对于函数=16,当=5时,把它代人函数解析式,得=16×5=80(元).=80叫做当自变量=5时的函数值.4.作业课本P34练习第1,2,3.5、课后反思: