北京市窦店中学七年级数学下册 8.7.4平行线的判定教案 北京课改版VIP免费

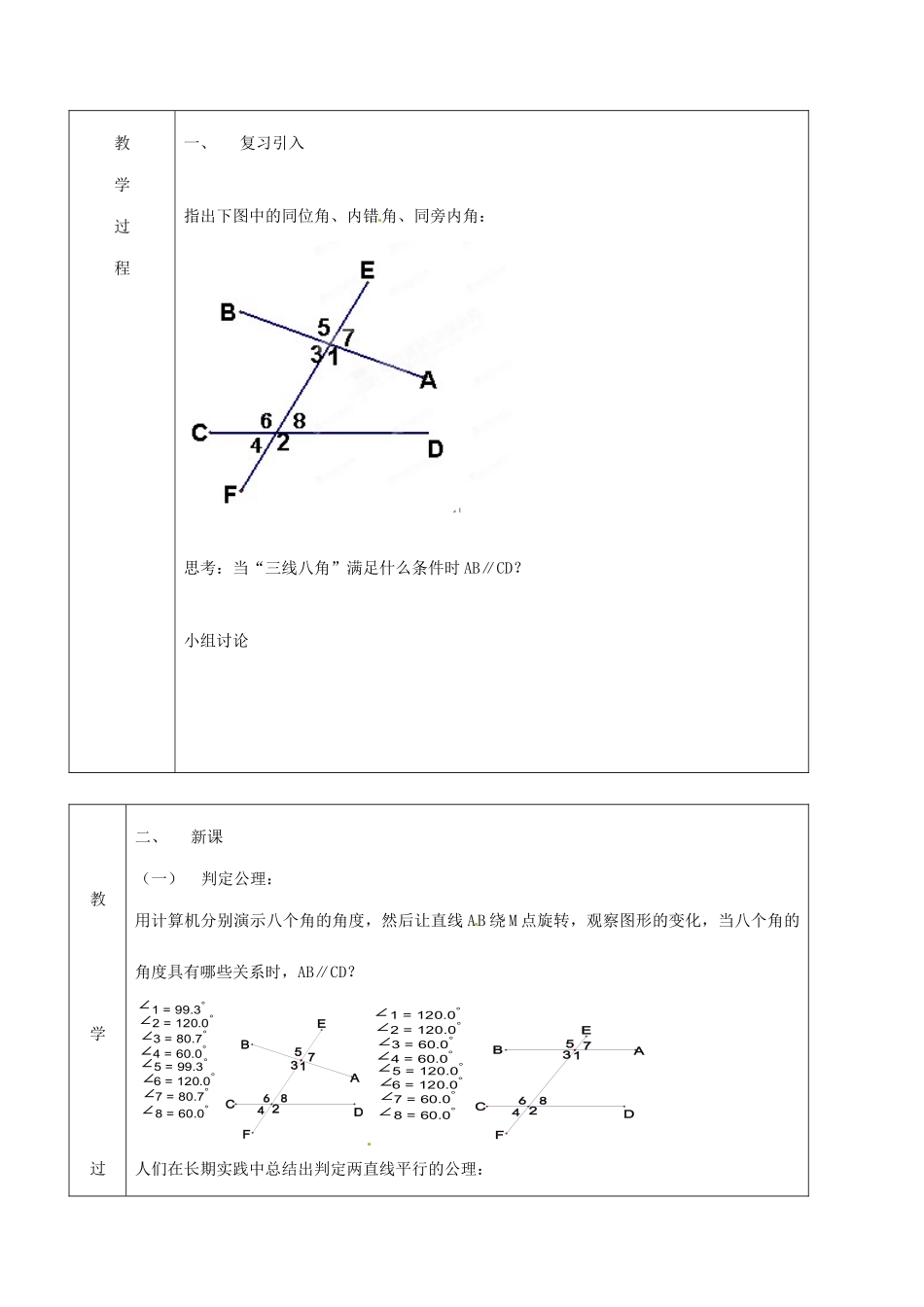
学科数学班级任课教师课题8.7.4平行线的判定课型新课日期学习目标：1、两直线被第三条直线所截时能够熟练的识别同位角、内错角、同旁内角。2、掌握平行线的判定公理和定理。3、会运用判定公理和定理判定两直线平行。学习重点平行线的判定方法。学习难点平行线判定公理和定理的得出及正确应用。教具学具多媒体、教材、三角板教学方法演示法、观察法、研讨法教学过程一、复习引入指出下图中的同位角、内错角、同旁内角：思考：当“三线八角”满足什么条件时AB∥CD？小组讨论教学过二、新课（一）判定公理：用计算机分别演示八个角的角度，然后让直线AB绕M点旋转，观察图形的变化，当八个角的角度具有哪些关系时，AB∥CD？578=60.07=80.76=120.05=99.34=60.03=80.71=99.32=120.086412BCDEFA3578=60.07=60.06=120.05=120.04=60.03=60.01=120.02=120.086412BCDEFA3人们在长期实践中总结出判定两直线平行的公理：程公理：两条直线被第三条直线所截，如果同位角相等，那么两直线平行（简记为：同位角相等，两直线平行）。表示为：∵∠1=∠2∴AB∥CD（二）判定定理1、如上图：当内错角∠1=∠6时，你能推出AB∥CD吗？生：简述推理过程：∵∠1=∠5（对顶角相等）且∠1=∠6（已知）∴∠5=∠6（等量代换）∴AB∥CD（同位角相等，两直线平行）由此得到：定理1：两条直线被第三条直线所截，如果内错角相等，那么两直线平行（简记为：内错角相等，两直线平行）表示为：∵∠1=∠6∴AB∥CD。2、类似还给以推出：（生：简述定理2推导过程。）定理2：两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行（简记为：同旁内角互补，两直线平行）表示为：∵∠1+∠8=180°∴AB∥CD教学过程（三）例题分析三、小结：平行线的判定方法：1、同位角相等，两直线平行。2、内错角相等，两直线平行。3、同旁内角互补，两直线平行。布置作业必做：书P135——练习选做：课改P77——78板书设计：平行线的判定1、公理：例1：例32、定理1定理2例2：课后自评与反思：