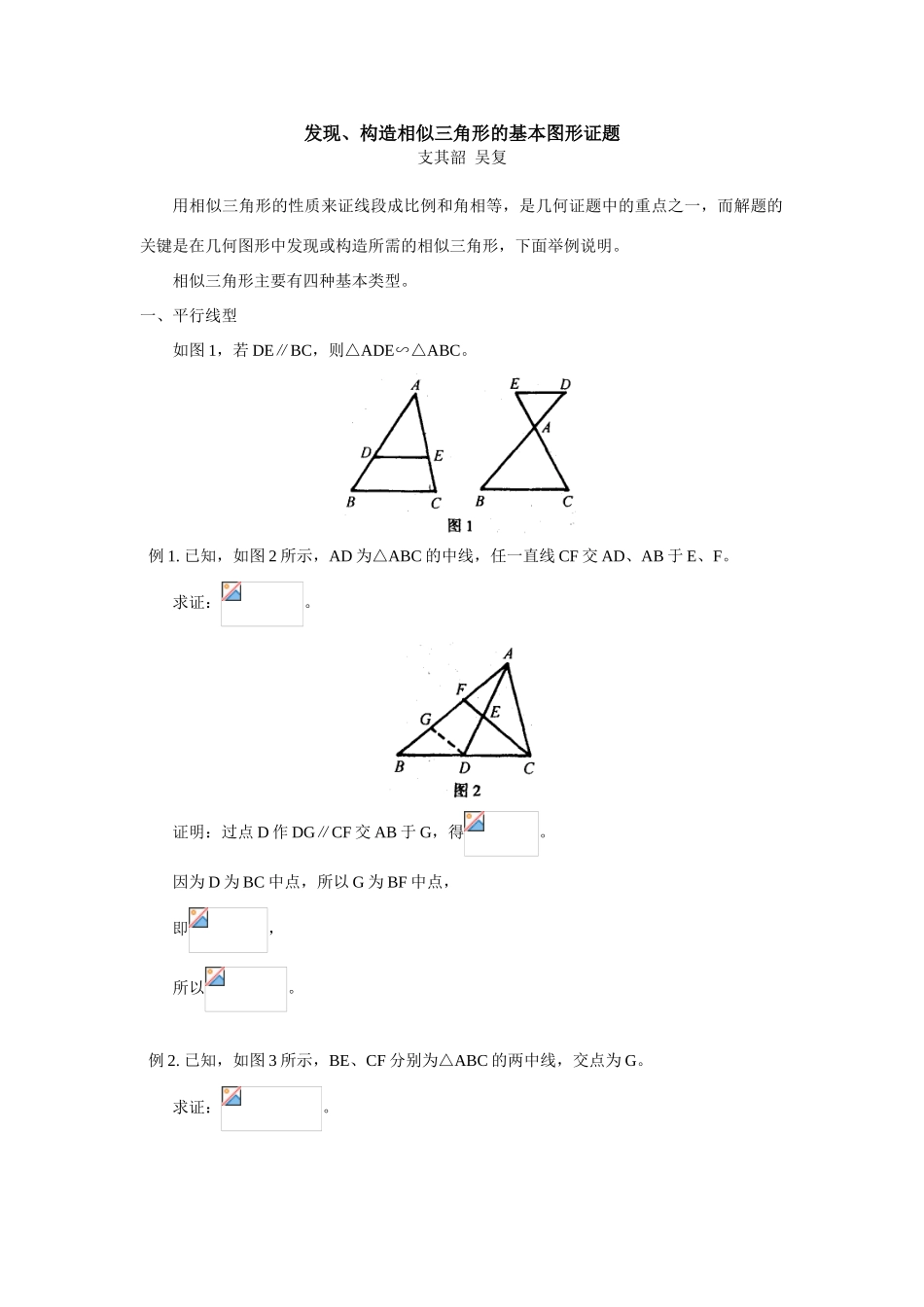
发现、构造相似三角形的基本图形证题支其韶吴复用相似三角形的性质来证线段成比例和角相等,是几何证题中的重点之一,而解题的关键是在几何图形中发现或构造所需的相似三角形,下面举例说明。相似三角形主要有四种基本类型。一、平行线型如图1,若DE∥BC,则△ADE∽△ABC。例1.已知,如图2所示,AD为△ABC的中线,任一直线CF交AD、AB于E、F。求证:。证明:过点D作DG∥CF交AB于G,得。因为D为BC中点,所以G为BF中点,即,所以。例2.已知,如图3所示,BE、CF分别为△ABC的两中线,交点为G。求证:。证明:连结EF。因为EF为△ABC的中位线,所以EF∥BC且EF=,所以。例3.已知,如图4所示,在△ABC中,直线MN交AB、AC和BC的延长线于X、Y、Z。求证:=1。证明:过点C作CD∥BA交YZ于D,则,,所以。二、相交线型如图5,若∠1=∠B,则可由公共角或对顶角得△ADE∽△ABC。例4.已知,如图6所示,△ABC中,AB=AC,D为AB上的点,E为AB延长线上的点,且。求证:BC平分∠DCE。分析:本题欲证∠BCD=∠BCE。由AB=AC可得∠ABC=∠ACB,而∠BCD=∠ACB-∠ACD,∠BCE=∠ABC-∠BEC,则只需证明∠ACD=∠AEC,而这一性质一出现可知通过相交线型的相似三角形进行证明,且只需证∠ACD=∠AEC的等价条件,而由和AB=AC,即可证出。例5.已知,如图7所示,CD为Rt△ABC的高,E为CD的中点,AE的延长线交BC于F,FG⊥AB于G。求证:。解析:欲证相乘两线段FC和FB重叠,则可通过添加相交线型相似三角形证明。由∠FGB=和∠FCA=可知延长GF交AC延长线于H后可得△HCF∽△BGF,CF·BF=GF·HF,再与结论比较可知应转化成证GF=HF,但由CD∥HG,又出现了三角形中的平行线段,则又可通过平行线型的相似三角形进行证明,从而有。已知CE=DE,故GF=HF即可证出。三、旋转型如图8,若∠BAD=∠CAE,则△ADE绕点A旋转一定角度后与△ABC构成平行线型的相似三角形。如图9,直角三角形中的相似三角形,若∠ACB=,AB⊥CD,则△ACD∽△CBD∽△ABC。例6.已知,如图10所示,D为△ABC内的一点,E为△ABC外的一点,且∠EBC=∠DBA,∠ECB=∠DAB。求证:DB·AC=AB·DE。证明:(简)由已知两对角分别相等,可证出△DBA∽△EBC。所以。由∠ABC=∠DBE,可证△ABC∽△DBE,所以,即DB·AC=AB·DE。例7.已知,如图11所示,F为正方形ABCD的边AB的中点,E为AD上的一点,AE=AD,FG⊥CE于G。求证:。证明:(简)连结EF、CF。由AE=,AF=BF=AB,四边形ABCD为正方形,得。因为∠A=∠B=,所以△EFA∽△FCB,∠1=∠2。因为∠2+∠3=,∠1+∠3=,所以∠EFC=。因为FG⊥CE,所以。若所证线段比例式(或等积式)的各线段明显不在两个相似三角形中,则设法等积代换、等线段代换、等比代换,使代换后的四线段含于两相似三角形中,若较复杂的题目即使作等量代换也无济于事,则需构造新的图形才能找出适当的等量代换。特别是欲证“,且m、a、b在同一直线上”的这类问题,往往要设法把线段m转换到另一位置上,从而找到相似三角形。例8.已知,如图12所示,在平行四边形ABCD中,O为对角线BD上的点,过O作直线分别交DC、AB于M、N,交AD的延长线于E,交CB的延长线于F。求证:OE·ON=OM·OF。证明:因为EA∥CF,所以∠E=∠F。又因为∠1=∠2,所以△EOD∽△FOB,所以OE:OF=OD:OB,同理可证△DOM∽△BON,所以OM:ON=OD:OB得OE:OF=OM:ON,即OE·ON=OM·OF,注:本例用的是等比代换。