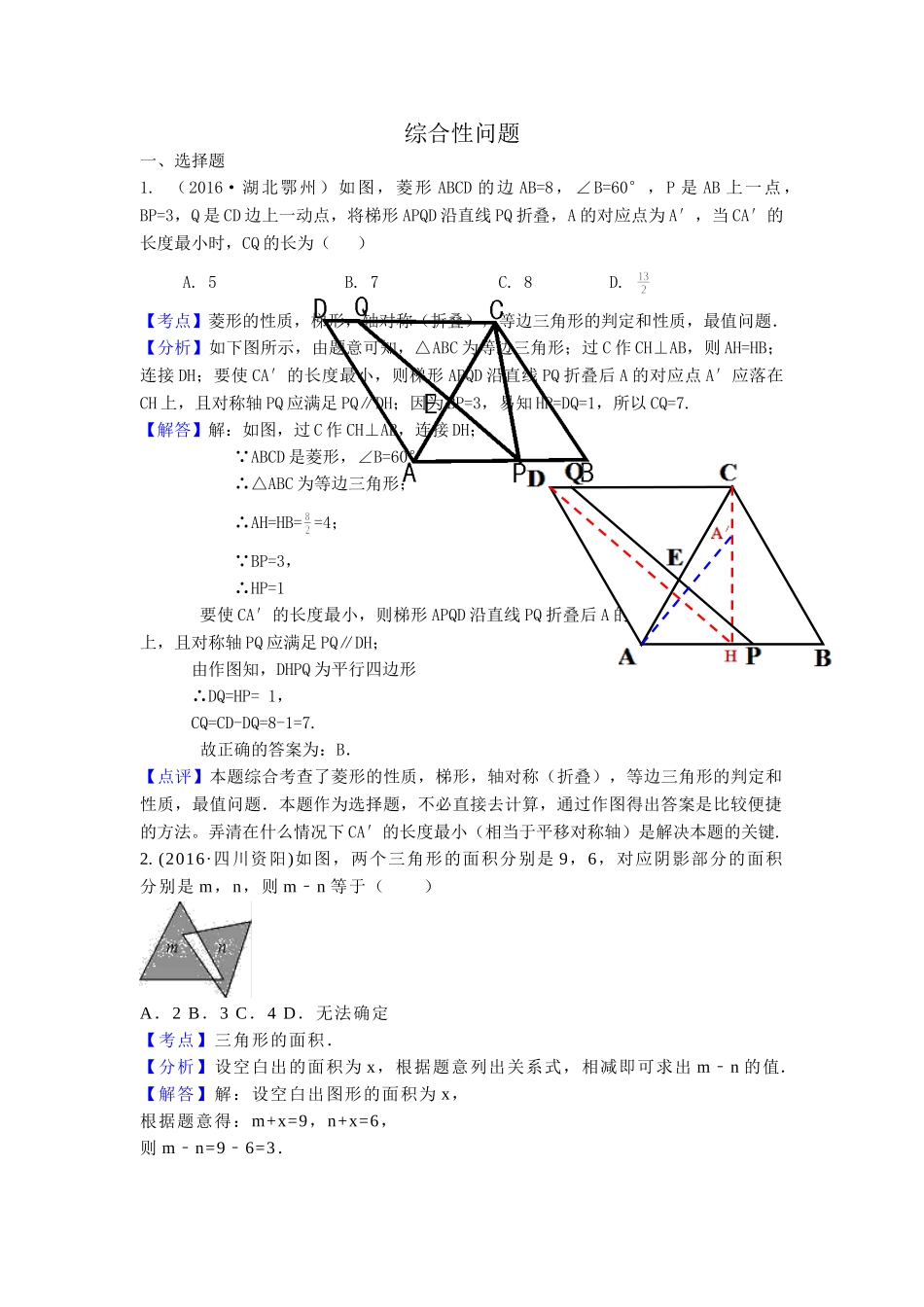
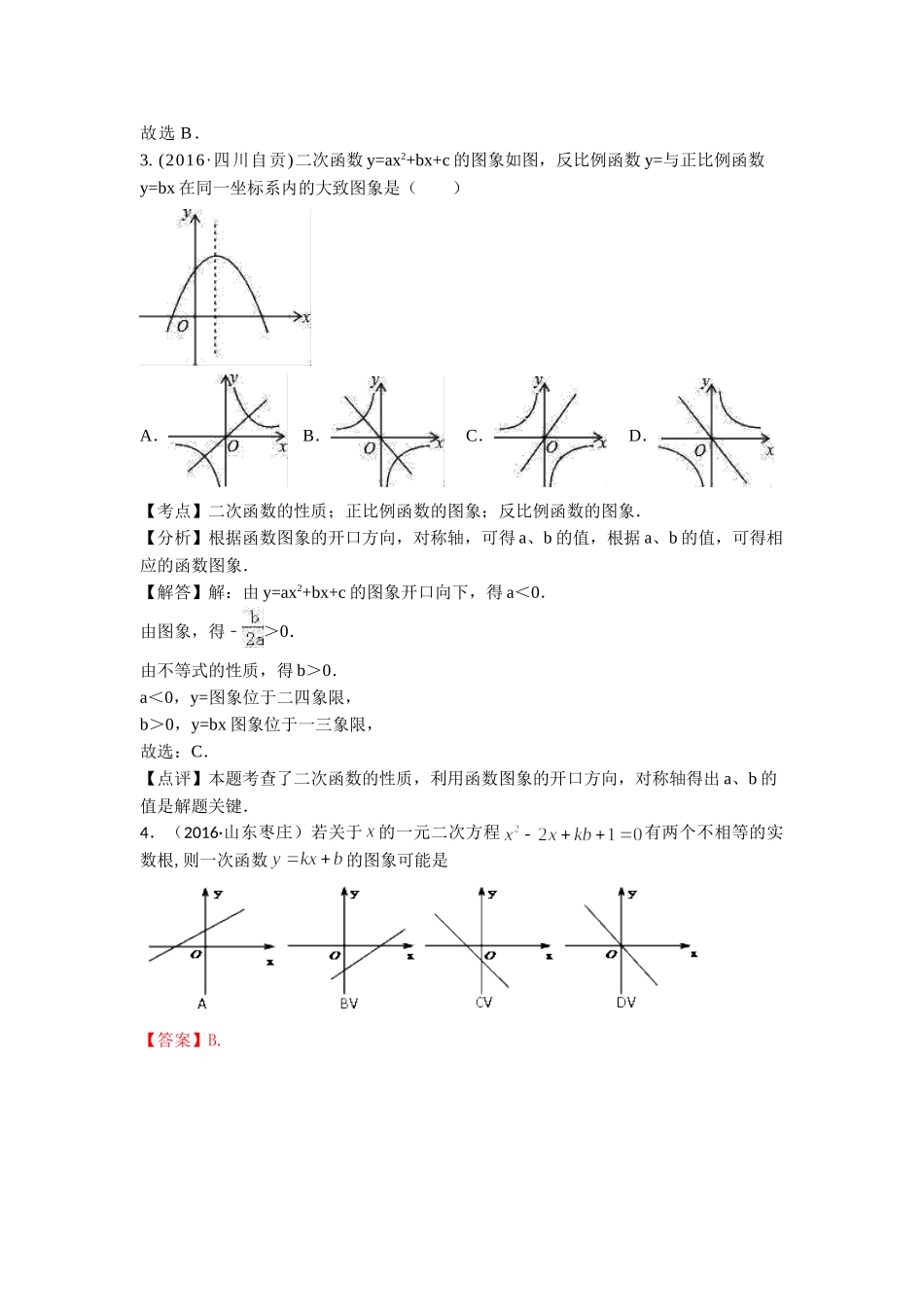
综合性问题一、选择题1.(2016·湖北鄂州)如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为()A.5B.7C.8D.【考点】菱形的性质,梯形,轴对称(折叠),等边三角形的判定和性质,最值问题.【分析】如下图所示,由题意可知,△ABC为等边三角形;过C作CH⊥AB,则AH=HB;连接DH;要使CA′的长度最小,则梯形APQD沿直线PQ折叠后A的对应点A′应落在CH上,且对称轴PQ应满足PQ∥DH;因为BP=3,易知HP=DQ=1,所以CQ=7.【解答】解:如图,过C作CH⊥AB,连接DH; ABCD是菱形,∠B=60°∴△ABC为等边三角形;∴AH=HB==4; BP=3,∴HP=1要使CA′的长度最小,则梯形APQD沿直线PQ折叠后A的对应点A′应落在CH上,且对称轴PQ应满足PQ∥DH;由作图知,DHPQ为平行四边形∴DQ=HP=1,CQ=CD-DQ=8-1=7.故正确的答案为:B.【点评】本题综合考查了菱形的性质,梯形,轴对称(折叠),等边三角形的判定和性质,最值问题.本题作为选择题,不必直接去计算,通过作图得出答案是比较便捷的方法。弄清在什么情况下CA′的长度最小(相当于平移对称轴)是解决本题的关键.2.(2016·四川资阳)如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则mn﹣等于()A.2B.3C.4D.无法确定【考点】三角形的面积.【分析】设空白出的面积为x,根据题意列出关系式,相减即可求出mn﹣的值.【解答】解:设空白出图形的面积为x,根据题意得:m+x=9,n+x=6,则mn=96=3﹣﹣.故选B.3.(2016·四川自贡)二次函数y=ax2+bx+c的图象如图,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是()A.B.C.D.【考点】二次函数的性质;正比例函数的图象;反比例函数的图象.【分析】根据函数图象的开口方向,对称轴,可得a、b的值,根据a、b的值,可得相应的函数图象.【解答】解:由y=ax2+bx+c的图象开口向下,得a<0.由图象,得﹣>0.由不等式的性质,得b>0.a<0,y=图象位于二四象限,b>0,y=bx图象位于一三象限,故选:C.【点评】本题考查了二次函数的性质,利用函数图象的开口方向,对称轴得出a、b的值是解题关键.4.(2016·山东枣庄)若关于的一元二次方程有两个不相等的实数根,则一次函数的图象可能是【答案】B.考点:根的判别式;一次函数的性质.二、填空题1.(2016·湖北鄂州)如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点。当△APB为直角三角形时,AP=.【考点】外接圆,切线,直角三角形的判定,勾股定理,三角函数,分类讨论思想.【分析】确定P点在直线l上的位置是解决本题的关键。要使△APB为直角三角形,我们就联想到以AB为直径的外接圆,但AB也有可能为直角边,所以要分类讨论。我们将满足条件的P逐一画在图上。如图,P1,P2在以O为圆心的外接圆上,P1,P2在⊙O的切线上,再根据题目的已知条件逐一解答即可。【解答】解:分类讨论如下:(1)在Rt△AP1B中, ∠1=120°,OP1=OB,∴∠OBP1=∠OP1B=30°,∴AP1=AB=×6=3;(2)在Rt△AP2B中, ∠1=120°,OP2=OB,∴∠P2BO=∠OP2B=60°,∴AP2=AB=cos∠OBP2×6=×6=3;(3)P3B为以B为切点的⊙O的切线, ∠1=120°,OP2=OB,∴∠P2BO=∠OP2B=60°,∴∠P3OB=60°,在Rt△OP3B中,∴BP3=tan∠P3OB×3=×3=3;在Rt△AP3B中,AP3===3;(4)P4B为以A为切点的⊙O的切线, ∠1=120°,OP1=OA,∴∠P1AO=∠OP1A=60°,∴∠P4OA=60°,在Rt△OP4A中,∴AP4=tan∠P4OA×3=×3=3.综上,当△APB为直角三角形时,AP=3,或3,或3.故答案为:3或3或3.【点评】本题考查了外接圆,切线,直角三角形的判定,勾股定理,三角函数,分类讨论思想.注意分类讨论思想的运用;本题难度虽然不大,但容易遗漏.四种情况中,有两种情况的结果相同。2.(2016.咸宁)如图,边长为4的正方形ABCD内接于⊙O,点E是AB上的一动点(不与A、B重合),点F是BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有下列结论:①AE=BF;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小...