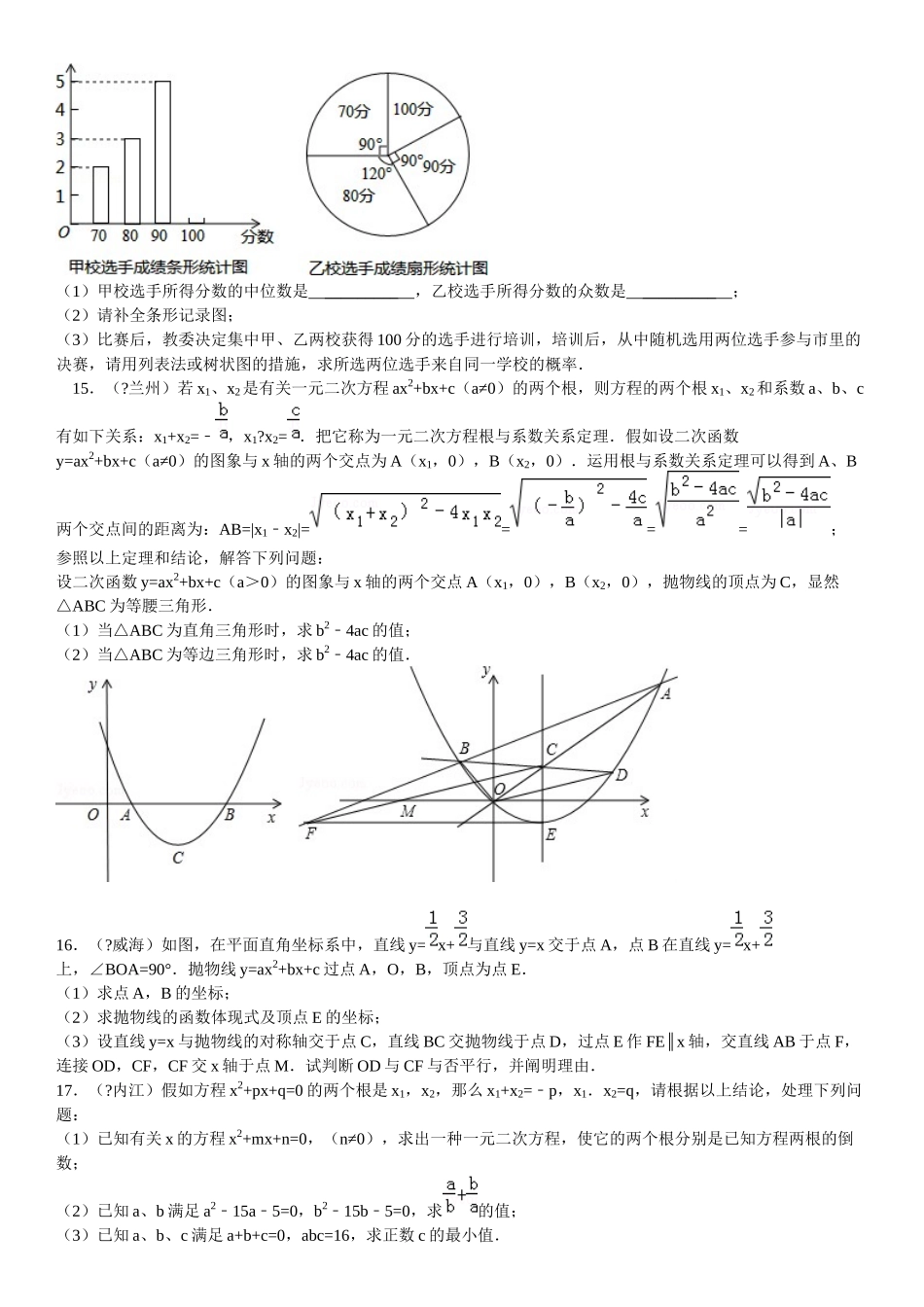
自主招生数学试题一.选择题(共6小题)1.已知函数,若使y=k成立的x值恰好有三个,则k的值为()A.0B.1C.2D.32.假如|xa|=a|x|﹣﹣(x≠0,x≠a),那么=()A.2aB.2xC.2a﹣D.2x﹣3.a,b,c为有理数,且等式成立,则2a+999b+1001c的值是()A.1999B.C.D.不能确定4.(?莒南县一模)如图,两个反比例函数y=和y=(其中k1>k2>0)在第一象限内的图象依次是C1和C2,设点P在C1上,PCx⊥轴于点C,交C2于点A,PDy⊥轴于点D,交C2于点B,则四边形PAOB的面积为()A.k1+k2B.k1k﹣2C.k1?k2D.5.如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,反复操作依次得到点P1,P2,…,则点P的坐标是()A.(,2)B.(,﹣2)C.(,﹣2)D.(0,2)6.如图,在半径为1的⊙O中,∠AOB=45°,则sinC的值为()A.B.C.D.二.填空题(共7小题)7.三个数a、b、c的积为负数,和为正数,且,则ax3+bx2+cx+1的值是_________.8.如图正方形ABCD中,E是BC边的中点,AE与BD相交于F点,△DEF的面积是1,那么正方形ABCD的面积是_________.9.(?沐川县二模)如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn1﹣在射线OB上,且A1B1A∥2B2A∥3B3…A∥∥n1﹣Bn1﹣,A2B1A∥3B2A∥4B3…A∥∥nBn1﹣,△A1A2B1,△A2A3B2,…,△An1﹣AnBn1﹣为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为_________;面积不不小于的阴影三角形共有_________个.10.你见过像,,…这样的根式吗?这一类根式叫做复合二次根式.有某些复合二次根式可以化简,如.请用上述措施化简:=_________.11.不等式组有六个整数解,则a的取值范围为_________.12.小明是一位刻苦学习、勤于思索、勇于创新的同学,一天他在解方程x2=1﹣时,突发奇想:x2=1﹣在实数范围内无解,假如存在一种数i,使i2=1﹣,那么若x2=1﹣,则x=±i,从而x=±i是方程x2=1﹣的两个根.据此可知:①i可以运算,例如:i3=i2?i=1×i=i﹣﹣,则i=_________,②方程x22x+2=0﹣的两根为_________(根用i表达)13.(?日照)如右图,直线AB交双曲线于A、B,交x轴于点C,B为线段AC的中点,过点B作BMx⊥轴于M,连结OA.若OM=2MC,SOAC△=12.则k的值为_________.三.解答题(共7小题)14.在“学科能力”展示活动中,某区教委决定在甲、乙两校举行“学科能力”比赛,为此甲、乙两学校都选派相似人数的选手参与,比赛结束后,发现每名参赛选手的成绩都是70分、80分、90分、l00分这四种成绩中的一种,并且甲、乙两校的选手获得100分的人数也相等.现根据甲、乙两校选手的成绩绘制如下两幅不完整记录图:(1)甲校选手所得分数的中位数是_________,乙校选手所得分数的众数是_________;(2)请补全条形记录图;(3)比赛后,教委决定集中甲、乙两校获得100分的选手进行培训,培训后,从中随机选用两位选手参与市里的决赛,请用列表法或树状图的措施,求所选两位选手来自同一学校的概率.15.(?兰州)若x1、x2是有关一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=﹣,x1?x2=.把它称为一元二次方程根与系数关系定理.假如设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).运用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1x﹣2|====;参照以上定理和结论,解答下列问题:设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.(1)当△ABC为直角三角形时,求b24ac﹣的值;(2)当△ABC为等边三角形时,求b24ac﹣的值.16.(?威海)如图,在平面直角坐标系中,直线y=x+与直线y=x交于点A,点B在直线y=x+上,∠BOA=90°.抛物线y=ax2+bx+c过点A,O,B,顶点为点E.(1)求点A,B的坐标;(2)求抛物线的函数体现式及顶点E的坐标;(3)设直线y=x与抛物...