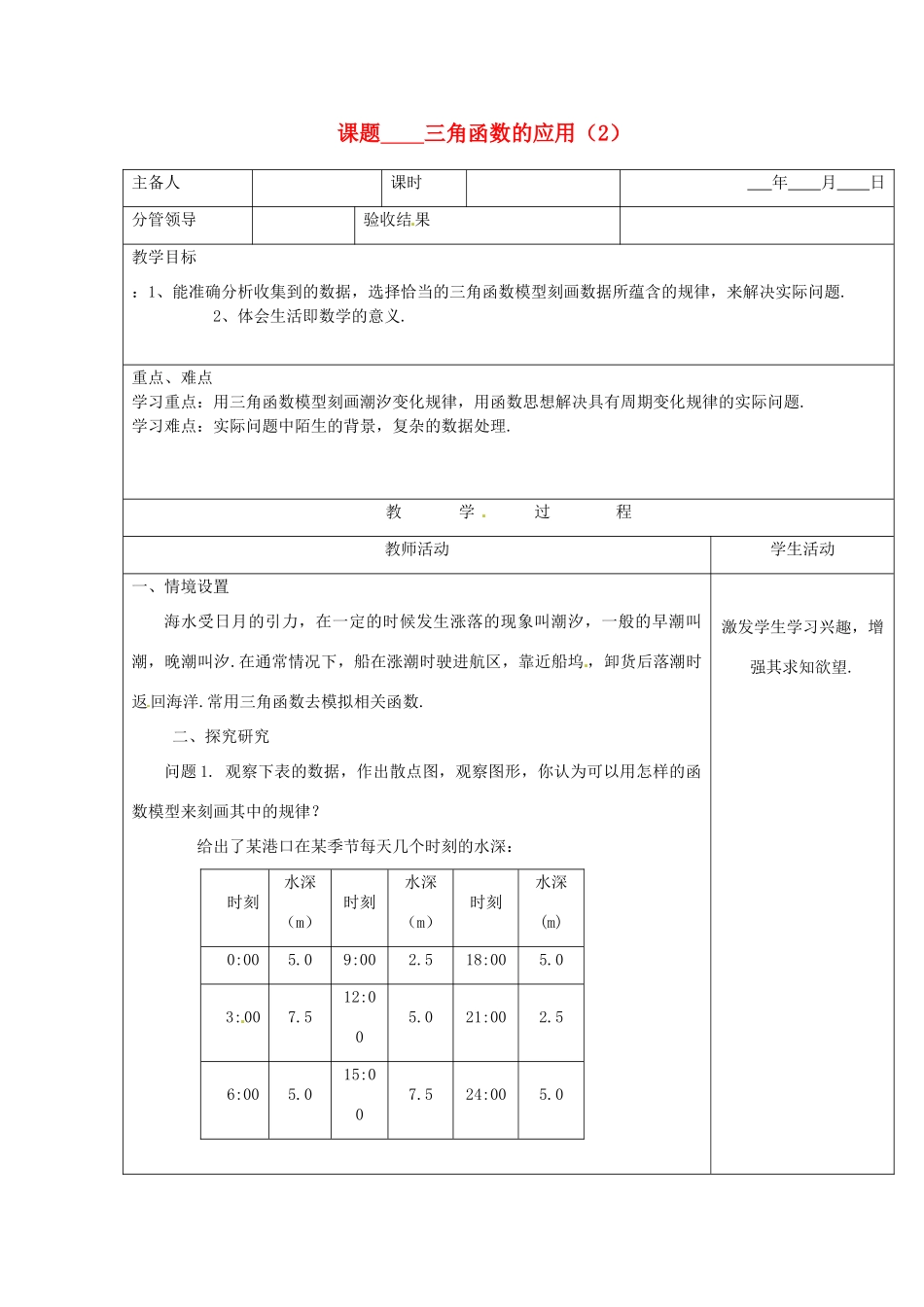
课题三角函数的应用(2)主备人课时年月日分管领导验收结果教学目标:1、能准确分析收集到的数据,选择恰当的三角函数模型刻画数据所蕴含的规律,来解决实际问题.2、体会生活即数学的意义.重点、难点学习重点:用三角函数模型刻画潮汐变化规律,用函数思想解决具有周期变化规律的实际问题.学习难点:实际问题中陌生的背景,复杂的数据处理.教学过程教师活动学生活动一、情境设置海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般的早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航区,靠近船坞,卸货后落潮时返回海洋.常用三角函数去模拟相关函数.二、探究研究问题1.观察下表的数据,作出散点图,观察图形,你认为可以用怎样的函数模型来刻画其中的规律?给出了某港口在某季节每天几个时刻的水深:时刻水深(m)时刻水深(m)时刻水深(m)0:005.09:002.518:005.03:007.512:005.021:002.56:005.015:007.524:005.0激发学生学习兴趣,增强其求知欲望.问题2.根据所得的函数模型,求出整点时的水深。问题3一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有1.5m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口待多久?问题4若船的吃水深度为4m,安全间隙为1.5m,该船在2:00开始卸货,吃水深度以每小时0.3m的速度减少,那么该船在什么时候必须停止卸货,将船驶向较深的水域?三、教学精讲例1:某港口相邻两次高潮发生时间间隔12h20min,低潮时入口处水的深度为2.8m,高潮时为8.4m,一次高潮发生在10月3日2:00。(1)若从10月3日0:00开始计算时间,选用一个三角函数来近似描述这个港口的水深d(m)和时间t(h)之间的函数关系;(2)求10月5日4:00水的深度;(3)求10月3日吃水深度为5m的轮船能进入港口的时间。例2.电流I(A)随时间t(s)变化的关系式是,,设,A=5。⑴求电流I变化的周期和频率;⑵当时,求电流I。⑶画出电流I(A)随时间t(s)变化的函数图象。学生独立思考,完成解答,并相互讨论、交流、评析.在学生自主思考,相互讨论完成本例题解答之后,写出具体的解答过程老师小结根据老师的引导启发析.,学生自主,建立恰当的函数模型,进行解答,然后交流、进行评四、巩固练习1、课本第65页练习2、从高出海面hm的小岛A处看正东方向有一只船B,俯角为看正南方向的一船C的俯角为,则此时两船间的距离为().A.B.C.D.六、自我测评:1、一个单摆如右图,摆角(弧度)作为时间(秒)的函数满足.(1)求最初位置的摆角(弧度);(2)求单摆的频率.(3)求多长时间单摆完成5次完整摆动(往复摆动一次称一次完整摆动)?2、大风车叶轮最高顶点离地面14.5米,风车轮直径为14米,车轮以每分钟2周的速度匀速转动.风叶轮顶点从离地面最低点经16秒后到达最高点.假设风叶轮离地面高度(米)与风叶轮离地面最低点开始转的时间(秒)建立一个数学模型,用函数来表示,试求出其中四个参数的值.3、下表是某市1975-2005年月平均气温(℃)月份123456789101112平均-5.9-3.32.29.315.120.322.822.218.211.94.3-2.4气温(1)下列函数模型中最适合这些数据的是()A、B、C、D、(2)请再写出一个与上述所选答案等价的模型来描述这些数据.4、如图,某地一天从6时至14时的温度变化曲线近似满足函数(1)求这段时间的最大温差.(2)写出这段曲线的函数解析式小结1、用三角函数的图象与性质解决一些简单的实际问题,数学模型的建立很重要,实际的取值范围也必须引起注意.2、数学建模的过程应完整清晰,实际应用问题并不仅仅局限于三角函数中.板书设计回顾例1例2练习