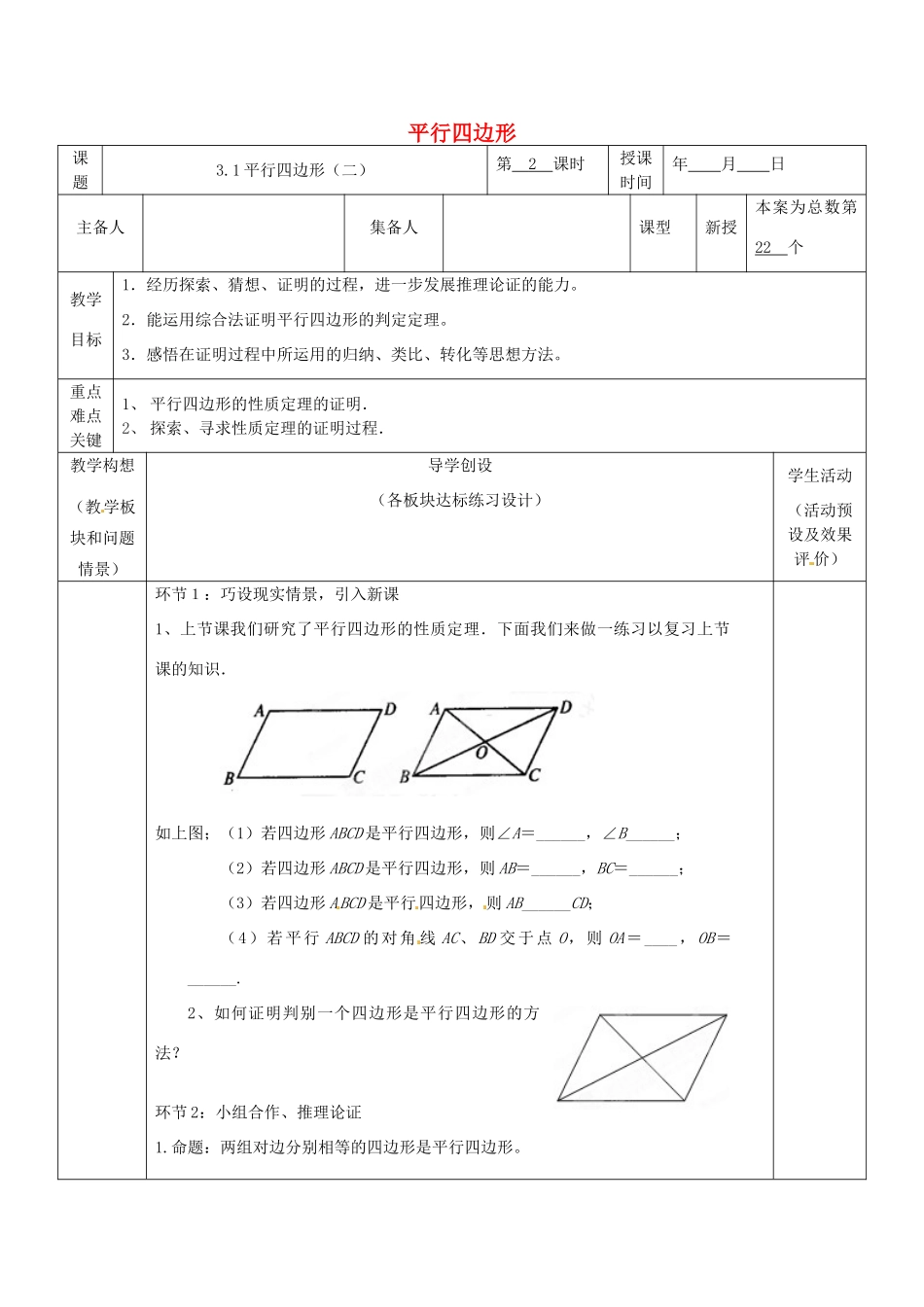
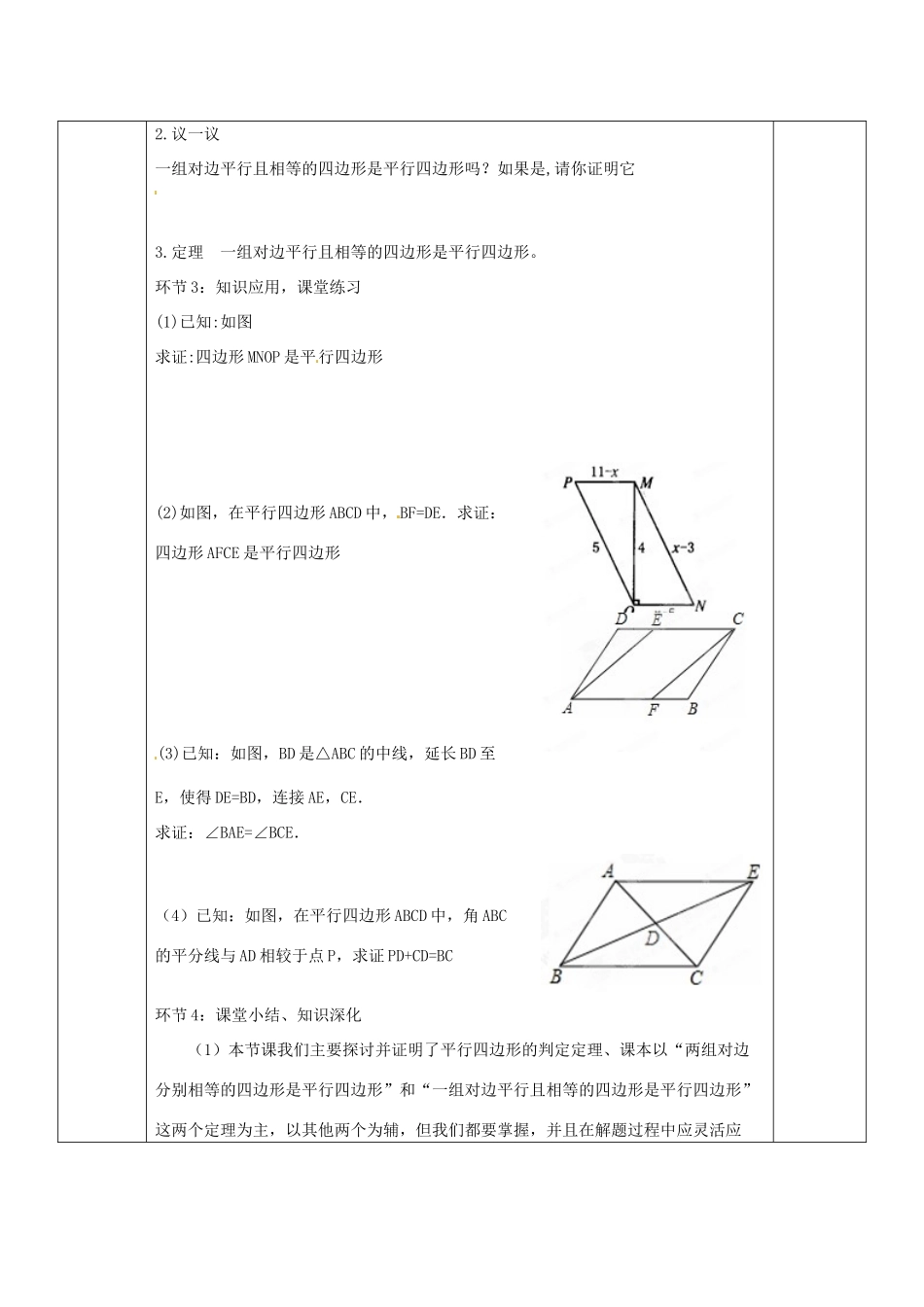
平行四边形课题3.1平行四边形(二)第2课时授课时间年月日主备人集备人课型新授本案为总数第22个教学目标1.经历探索、猜想、证明的过程,进一步发展推理论证的能力。2.能运用综合法证明平行四边形的判定定理。3.感悟在证明过程中所运用的归纳、类比、转化等思想方法。重点难点关键1、平行四边形的性质定理的证明.2、探索、寻求性质定理的证明过程.教学构想(教学板块和问题情景)导学创设(各板块达标练习设计)学生活动(活动预设及效果评价)环节1:巧设现实情景,引入新课1、上节课我们研究了平行四边形的性质定理.下面我们来做一练习以复习上节课的知识.如上图;(1)若四边形ABCD是平行四边形,则∠A=______,∠B______;(2)若四边形ABCD是平行四边形,则AB=______,BC=______;(3)若四边形ABCD是平行四边形,则AB______CD;(4)若平行ABCD的对角线AC、BD交于点O,则OA=____,OB=______.2、如何证明判别一个四边形是平行四边形的方法?环节2:小组合作、推理论证1.命题:两组对边分别相等的四边形是平行四边形。2.议一议一组对边平行且相等的四边形是平行四边形吗?如果是,请你证明它3.定理一组对边平行且相等的四边形是平行四边形。环节3:知识应用,课堂练习(1)已知:如图求证:四边形MNOP是平行四边形(2)如图,在平行四边形ABCD中,BF=DE.求证:四边形AFCE是平行四边形(3)已知:如图,BD是△ABC的中线,延长BD至E,使得DE=BD,连接AE,CE.求证:∠BAE=∠BCE.(4)已知:如图,在平行四边形ABCD中,角ABC的平分线与AD相较于点P,求证PD+CD=BC环节4:课堂小结、知识深化(1)本节课我们主要探讨并证明了平行四边形的判定定理、课本以“两组对边分别相等的四边形是平行四边形”和“一组对边平行且相等的四边形是平行四边形”这两个定理为主,以其他两个为辅,但我们都要掌握,并且在解题过程中应灵活应用。(2)平行四边形的判定定理定理:两组对角分别相等的四边形是平行四边形.定理:两组对边分别相等的四边形是平行四边形.定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.环节5:作业:本P77习题3.22教后感