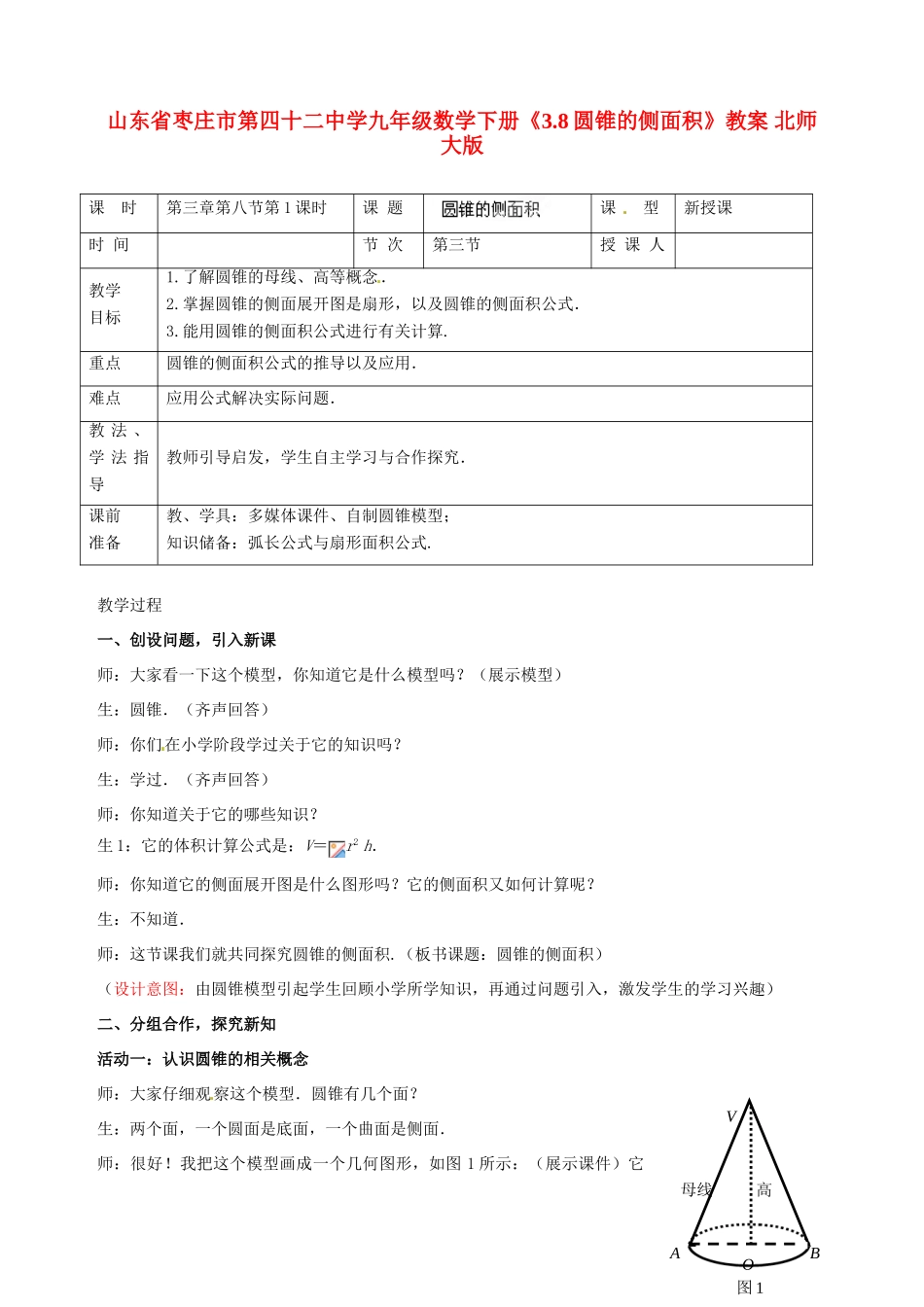
山东省枣庄市第四十二中学九年级数学下册《3.8圆锥的侧面积》教案北师大版教学过程一、创设问题,引入新课师:大家看一下这个模型,你知道它是什么模型吗?(展示模型)生:圆锥.(齐声回答)师:你们在小学阶段学过关于它的知识吗?生:学过.(齐声回答)师:你知道关于它的哪些知识?生1:它的体积计算公式是:V=r2h.师:你知道它的侧面展开图是什么图形吗?它的侧面积又如何计算呢?生:不知道.师:这节课我们就共同探究圆锥的侧面积.(板书课题:圆锥的侧面积)(设计意图:由圆锥模型引起学生回顾小学所学知识,再通过问题引入,激发学生的学习兴趣)二、分组合作,探究新知活动一:认识圆锥的相关概念师:大家仔细观察这个模型.圆锥有几个面?生:两个面,一个圆面是底面,一个曲面是侧面.师:很好!我把这个模型画成一个几何图形,如图1所示:(展示课件)它课时第三章第八节第1课时课题课型新授课时间节次第三节授课人教学目标1.了解圆锥的母线、高等概念.2.掌握圆锥的侧面展开图是扇形,以及圆锥的侧面积公式.3.能用圆锥的侧面积公式进行有关计算.重点圆锥的侧面积公式的推导以及应用.难点应用公式解决实际问题.教法、学法指导教师引导启发,学生自主学习与合作探究.课前准备教、学具:多媒体课件、自制圆锥模型;知识储备:弧长公式与扇形面积公式.A图1母线高OBV的最尖的部分是一个点,你知道叫什么吗?生:顶点.师:对!顶点.刚才我们观察模型时,知道底面是一个圆形,圆形一定有圆心.现在连接圆心与顶点,你知道这条线段叫什么吗?生:高.师:好!再连接圆锥的顶点和底面圆上任意一点,又得到一条线段,你还知道叫什么吗?生:母线.(个别同学回答)师:预习的同学都知道.看来大部分同学没有预习,希望大家今后养成预习的好习惯.我们继续了解母线.在图1中,VA和VB都是母线,现在大家思考一下,它们有什么大小关系?(学生自主探究)生1:VA=VB,因为△VOA和△VOB都是直角三角形,并且OA=OB,VO为公共边,所以Rt△VOA与Rt△VOB全等,所以VA=VB.师:很好!我们鼓励一下.实际上,圆锥的所有母线都是相等的.除了母线外,如果用r表示底面圆的半径,h表示圆锥的高,l表示母线的长,你还能得到它们之间有什么关系?生2:由勾股定理得,r2+h2=l2师:很好!这个公式有时候能用到,大家注意一下.实际上,我们可以把直角三角形绕着一条直角边旋转一圈就能得到一个圆锥.设计意图:通过模型使学生加深对基本概念的理解,为下一步推导公式打下基础.活动二:探究圆锥的侧面积师:现在大家注意观察,如果把这个无底面的圆锥模型沿着母线剪开,会得到一个什么图形呢?(找个学生动手操作,然后展示)生:扇形.师:我们要探究的圆锥的侧面积实际就是展开后得到的扇形的面积.现在请同学们默写出上节课我们学习的扇形的面积公式和弧长公式.(一个同学在黑板默写)生1:扇形面积,弧长公式师:大家检查他默写的对不对?生:对.师:看来上节课的知识掌握还可以.现在就利用这些公式探究圆锥的侧面积.(展示课件)设圆锥的母线长为l,底面圆的半径为r,如图2所示,给你几分钟时间,探究下面问题:(1)底面圆的周长是多少?(2)底面圆的周长与展开后得到的扇形的弧长有什么关系?(3)展开后得到的扇形的面积怎么计算?(学生小组讨论,探究学习,教师巡视指导)师:有结论的请举手?生1:底面圆的周长是2r,底面圆的周长与展开后的扇形的弧长相等,因此扇形面积为S=×2rl=rl师:大家同意他的结论吗?生:同意.师:非常好!这个公式S侧=rl,就是我们要得到的圆锥的侧面积公式.大家一定要熟记,特别是每个字母表示的意义.那么圆锥的全面积你会计算吗?生:S全=rl+r2师:圆锥的侧面积与底面积之和就是圆锥的全面积.现在大家想一想,在推导圆锥侧面积公式的过程中,关键点在哪?为什么?(学生讨论)生:我认为关键在于底面圆的周长与展开后的扇形的弧长相等.因为要求扇形面积,已经知道半径了,再求弧长就可以了,而弧长恰好就是底面圆的周长.师:他分析的有道理吗?生:有道理.师:很好!其实根据这一点,还可能求出展开后扇形的圆心角,甚至...