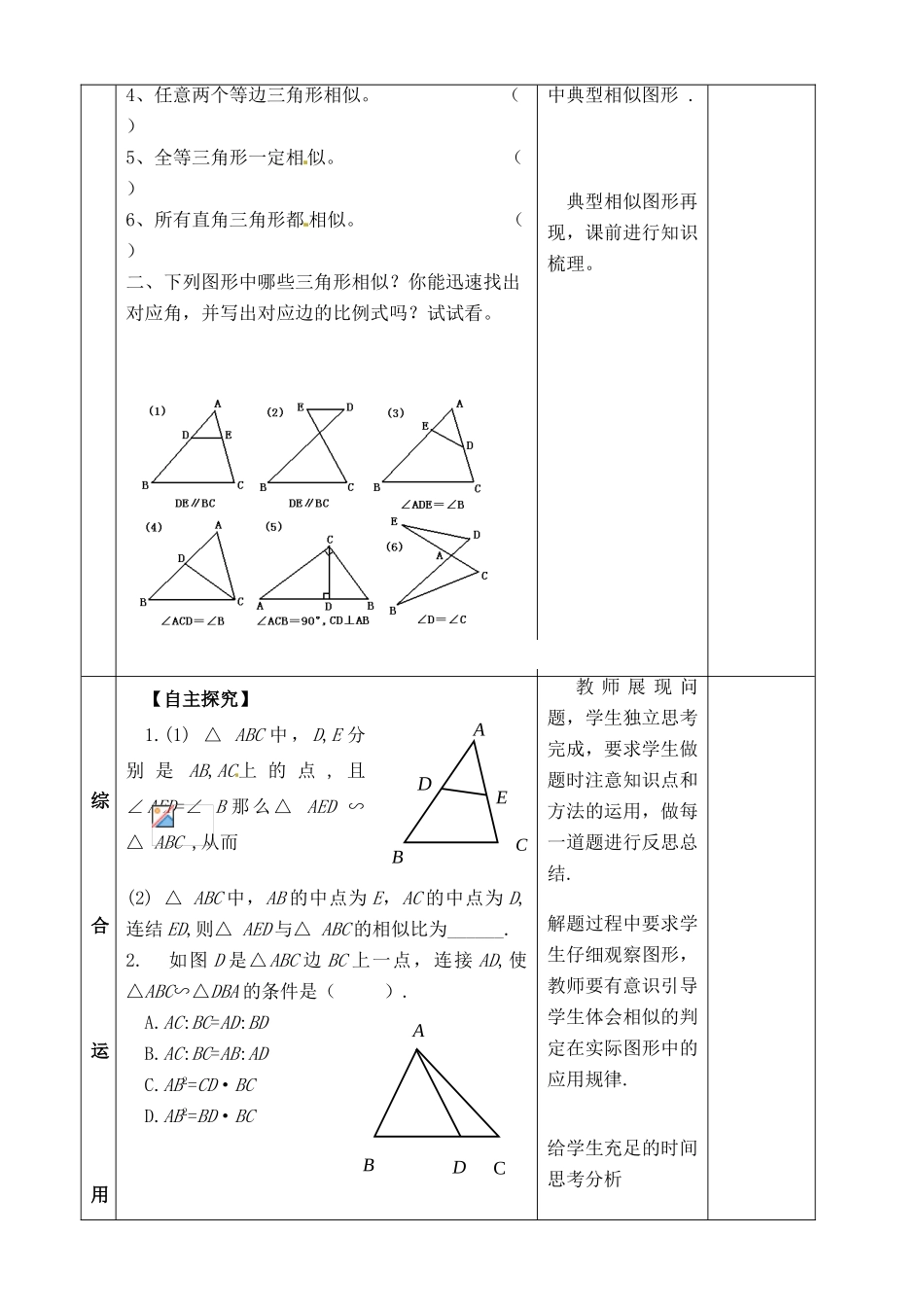
相似的判定一、【教材分析】教学目标知识技能1、进一步巩固相似三角形判定的知识,利用三角形相似,证明角相等,线段成比例,表示线段的长等.2、能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量物体内径)等的一些实际问题.3、通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力.过程方法学会与同学交流合作,培养团队精神,变他有为己有,培养把自己的想法与观点陈述给其他同学的语言表述能力.情感态度体验学习几何过程中成功的快乐,增强学习几何的信心与热情.教学重点相似三角形判定的灵活应用.教学难点把实际问题转化成相似三角形的数学模型.二、【教学流程】教学环节教学问题设计师生活动二次备课知识回顾一、判断:下列结论是否正确?说说你的理由。1、底角相等的两个等腰三角形相似。()2、有一个钝角相等的两个等腰三角形相似。()3、任意两个等腰直角三角形相似。()通过课前热身练习,让学生对知识进行回忆,进一步理解体会相似的定义以及相似的不同判定方法和集BCAED4、任意两个等边三角形相似。()5、全等三角形一定相似。()6、所有直角三角形都相似。()二、下列图形中哪些三角形相似?你能迅速找出对应角,并写出对应边的比例式吗?试试看。中典型相似图形.典型相似图形再现,课前进行知识梳理。综合运用【自主探究】1.(1)△ABC中,D,E分别是AB,AC上的点,且∠AED=∠B那么△AED∽△ABC,从而(2)△ABC中,AB的中点为E,AC的中点为D,连结ED,则△AED与△ABC的相似比为______.2.如图D是△ABC边BC上一点,连接AD,使△ABC∽△DBA的条件是().A.AC:BC=AD:BDB.AC:BC=AB:ADC.AB2=CD·BCD.AB2=BD·BC教师展现问题,学生独立思考完成,要求学生做题时注意知识点和方法的运用,做每一道题进行反思总结.解题过程中要求学生仔细观察图形,教师要有意识引导学生体会相似的判定在实际图形中的应用规律.给学生充足的时间思考分析ABCD3.D,E分别为△ABC的AB,AC上的点,且DE∥BC,∠DCB=∠A,把每两个相似的三角形称为一组,那么图中共有相似三角形_____组【组内交流】学生根据问题解决的思路和解题中所呈现的问题进行组内交流,归纳出方法、规律、技巧.【成果展示】通过学生思考梳理相似的判定知识运用.一生展示,其它小组补充完善,展示问题解决的方法,注重一题多解及解题过程中的共性问题,教师注意总结问题的深度和广度.直击中考1.(岳阳)如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm.球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到点D的位置.(1)求证:△BEF∽△CDF;(2)求CF的长.2.△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连结AM.求证:①△MAD∽△MEA②AM2=MD·ME教师展示问题,学生有针对性独立思考解答,完成后师生间展评.完常见的相似三角形的基本图形:师生梳理本课对内容的升华理解ACBDECAEDBM善整合你收获了什么?的知识点及及注意问——归结本节课所复习的内容,梳理知识,构建思维导图,凸显数学思想方法.生反思总结本课中的难点、重点及易错点,并在错题中整理所产生的问题.针对性问题师板书.认识作业必做题1.△ABC为锐角三角形,BD,CE为△的高.求证:△ADE∽△ABC(用两种方法证明).选做题2.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3BF⊥BP垂足是B请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似,则BM是多少?第一题学生课下独立完成,延续课堂.第二题课下交流讨论有选择性完成.以生为本,正视学生学习能力、认知水平等个体差异,让不同的学生都能学有所得,学有所成,体验学习带来的成功与快乐.(7)AOBEDCAOBEDCAOBEDCFPDCBAAOBEDC三、【板书设计】相似的判定复习常见的相似图形:四、【教后反思】我认为,数学复习课没有一个基本公认的课堂教学模式。复习课并非单纯的知识的重述,而应是知识点的重新整合、深化、升华。复习课更应重视发展学生的数学思维能力,巩固旧知,是为了获取新知,同时,要尽可能兼顾每一位不同学习层次的学生,要让每一个学...