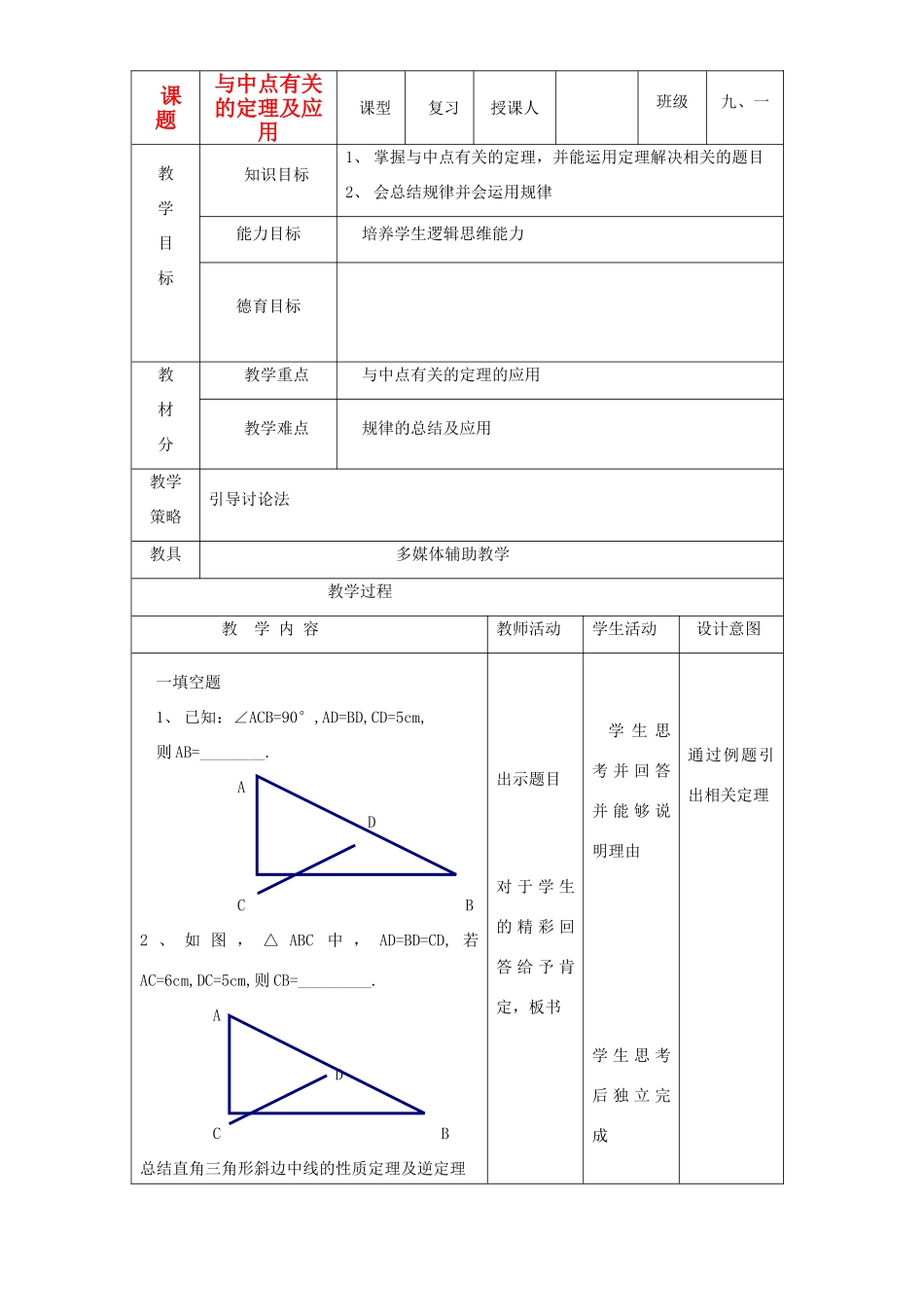
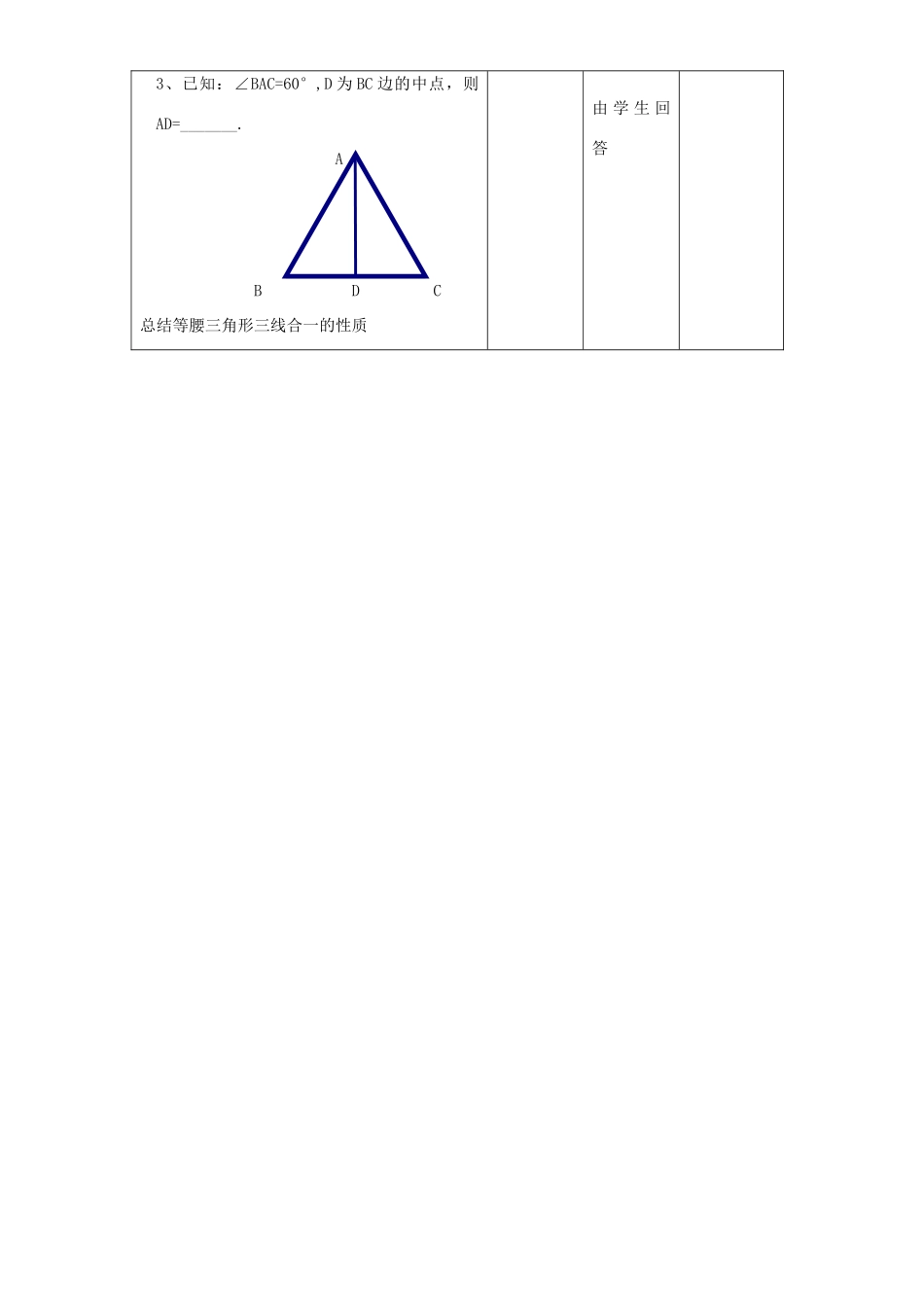
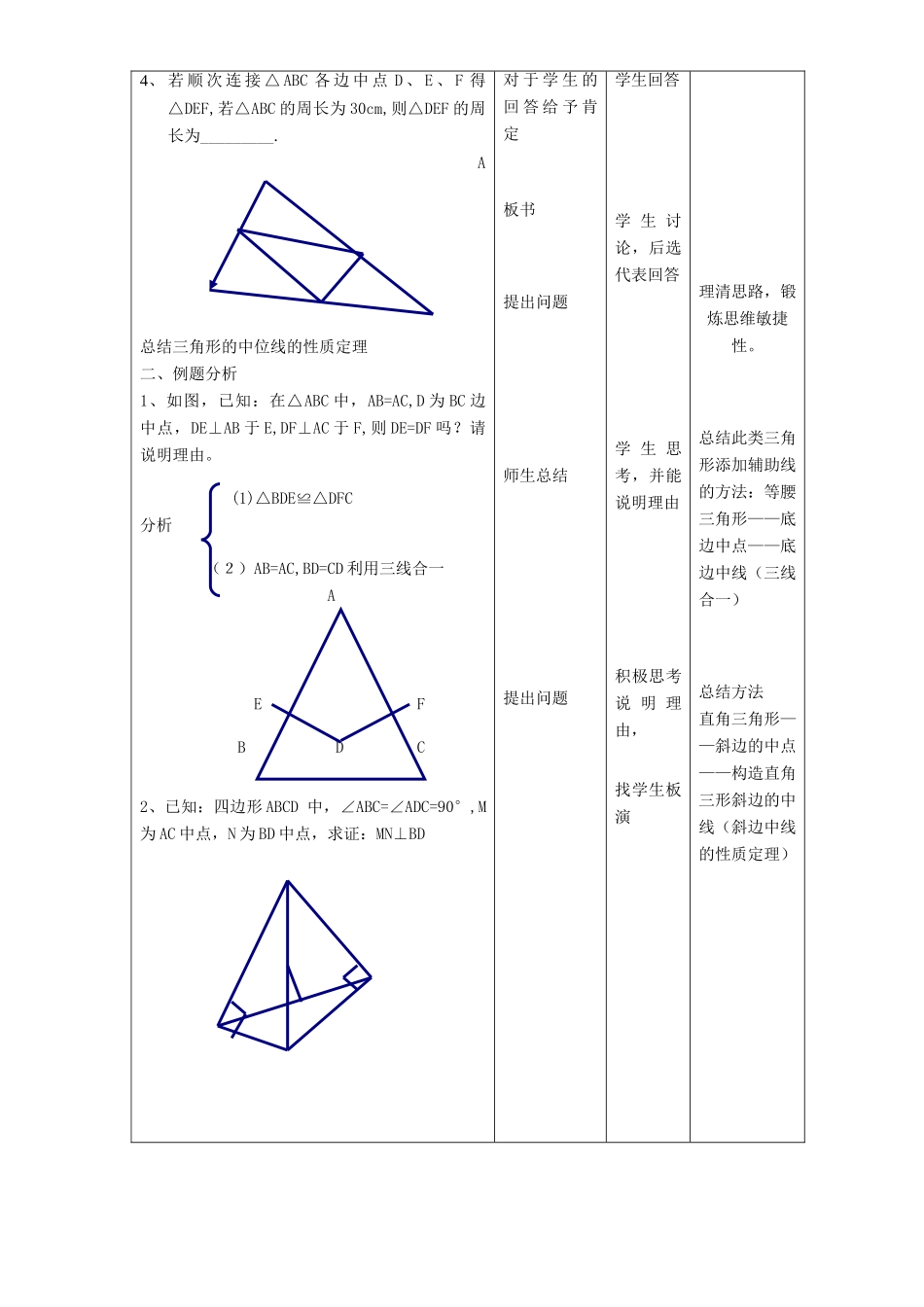
课题与中点有关的定理及应用课型复习授课人班级九、一教学目标知识目标1、掌握与中点有关的定理,并能运用定理解决相关的题目2、会总结规律并会运用规律能力目标培养学生逻辑思维能力德育目标教材分教学重点与中点有关的定理的应用教学难点规律的总结及应用教学策略引导讨论法教具多媒体辅助教学教学过程教学内容教师活动学生活动设计意图一填空题1、已知:∠ACB=90°,AD=BD,CD=5cm,则AB=________.ADCB2、如图,△ABC中,AD=BD=CD,若AC=6cm,DC=5cm,则CB=_________.ADCB总结直角三角形斜边中线的性质定理及逆定理出示题目对于学生的精彩回答给予肯定,板书学生思考并回答并能够说明理由学生思考后独立完成通过例题引出相关定理3、已知:∠BAC=60°,D为BC边的中点,则AD=_______.ABDC总结等腰三角形三线合一的性质由学生回答4、若顺次连接△ABC各边中点D、E、F得△DEF,若△ABC的周长为30cm,则△DEF的周长为_________.A总结三角形的中位线的性质定理二、例题分析1、如图,已知:在△ABC中,AB=AC,D为BC边中点,DE⊥AB于E,DF⊥AC于F,则DE=DF吗?请说明理由。(1)△BDE≌△DFC分析(2)AB=AC,BD=CD利用三线合一AEFBDC2、已知:四边形ABCD中,∠ABC=∠ADC=90°,M为AC中点,N为BD中点,求证:MN⊥BD对于学生的回答给予肯定板书提出问题师生总结提出问题学生回答学生讨论,后选代表回答学生思考,并能说明理由积极思考说明理由,找学生板演理清思路,锻炼思维敏捷性。总结此类三角形添加辅助线的方法:等腰三角形——底边中点——底边中线(三线合一)总结方法直角三角形——斜边的中点——构造直角三形斜边的中线(斜边中线的性质定理)教学内容教师活动学生活动设计意图2、已知:D、E分别是△ABC的边BC、AC上的点,且AE=CE,AD、BE交于点F,且BF=EF,求证:CD=2BD分析:EFCBD三:练习已知:如图,AB=AD=CD,AE=ED,求证:BC=2BE四、走近生活有一块三角形的土地,要平均分给四户人家,你能用2种以上的方法帮他们分开吗?教师引导讨论三种解题思路四种方法从而引导学生找出最简便方法让学生明白实际问题实际分析,并不是所有的题目都得靠总结的规律来做学生积极交流讨论并作答,总结添加辅助线的方法讨论交流再独立完成步骤学生交流如无时间可留作作业一般三角形——中点——中点,构造三角形中位线寻找简便方法实际应用ABC教学随笔板书设计与中点有关的性质定理及应用一、定理1、等腰三角形:三线合一2、直角三角形斜边中线的性质定理逆定理:2、三角形的中位线定理:二、应用1、等腰三角形——底边的中点——底边的中线(三线合一)2、直角三角形——斜边的中点——斜边的中线(性质定理)3、一般三角形——中点——中点(中位线的性质定理)例3图方法1、找对应线段2、减半总结应用33、加倍