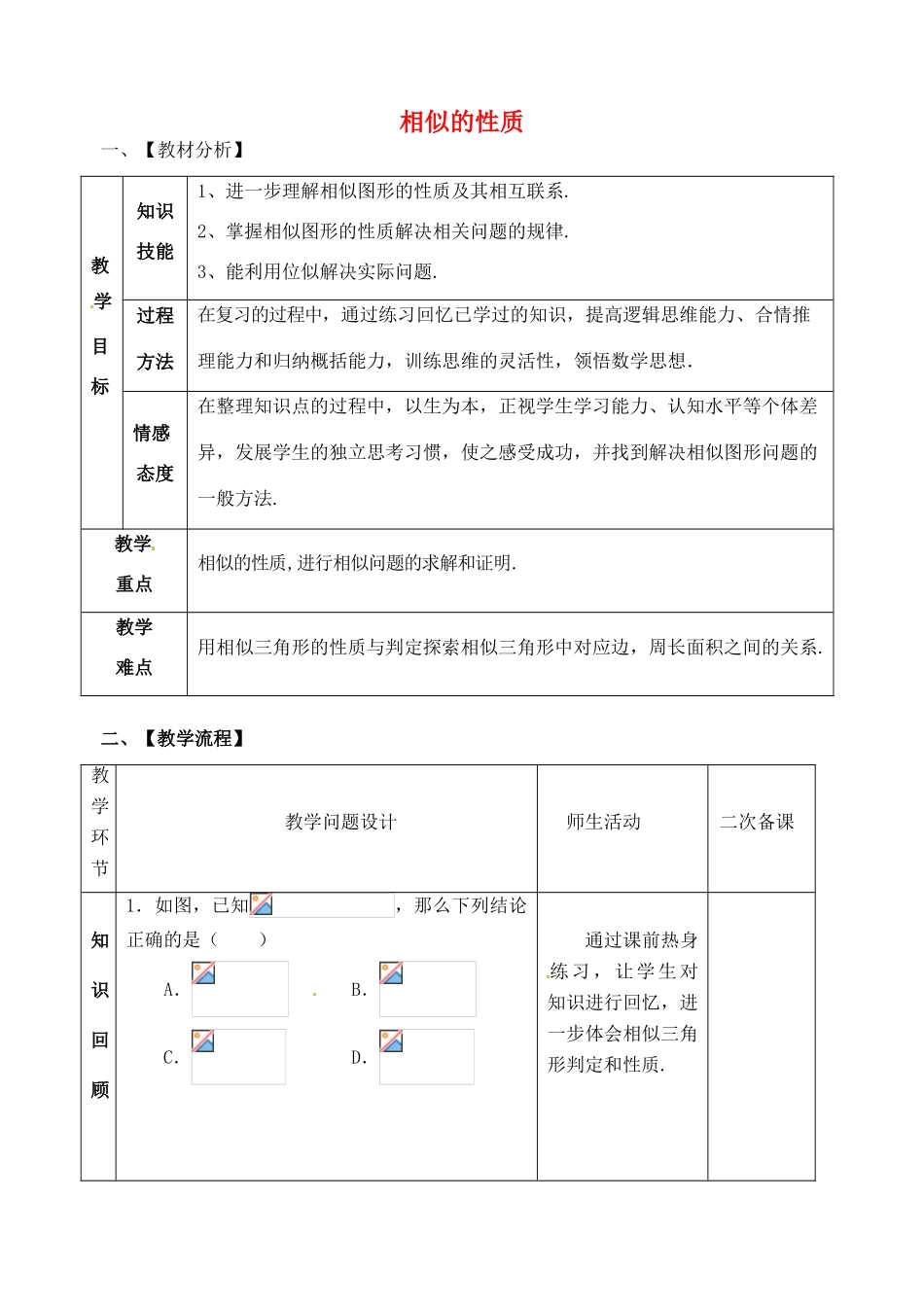
相似的性质一、【教材分析】教学目标知识技能1、进一步理解相似图形的性质及其相互联系.2、掌握相似图形的性质解决相关问题的规律.3、能利用位似解决实际问题.过程方法在复习的过程中,通过练习回忆已学过的知识,提高逻辑思维能力、合情推理能力和归纳概括能力,训练思维的灵活性,领悟数学思想.情感态度在整理知识点的过程中,以生为本,正视学生学习能力、认知水平等个体差异,发展学生的独立思考习惯,使之感受成功,并找到解决相似图形问题的一般方法.教学重点相似的性质,进行相似问题的求解和证明.教学难点用相似三角形的性质与判定探索相似三角形中对应边,周长面积之间的关系.二、【教学流程】教学环节教学问题设计师生活动二次备课知识回顾1.如图,已知,那么下列结论正确的是()A.B.C.D.通过课前热身练习,让学生对知识进行回忆,进一步体会相似三角形判定和性质.2.如图所示,给出下列条件:①;②;③;④.其中单独能够判定的个数为()A.1B.2C.3D.43.已知△ABC∽△DEF,且AB:DE=1:2,则△ABC的面积与△DEF的面积之比为()A.1:2B.1:4C.2:1D.4:14.如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:(1)DE=1,(2)△CDE∽△CAB,(3)△CDE的面积与△CAB的面积之比为1:4.其中正确的有:()A.0个B.1个C.2个D.3个概念再现,知识梳理.【自主探究】11.甲,乙两盏路灯底部间的距离是30米,一天上,当小华走到距路灯乙底部5米处时,发现教师展现问题,学生独立思考ABDCEF1题ACDB(第2题图)三、【板书设计】综合运用自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为米.2.如图,在已建立直角坐标系的4×4正方形方格纸中,△划格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是_______.3.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3,(1)求的值,(2)求BC的长【组内交流】学生根据问题解决的思路和解题中所呈现的问题进行组内交流,归纳出方法、规律、技巧.【成果展示】完成,要求学生做题时注意知识点和方法的运用,做每一道题进行反思总结.解题过程中要求学生仔细观察图形,教师要有意识引导学生体会相似的判定和性质在实际图形中的应用规律.给学生充足的时间思考分析通过学生思考梳理相似的性质的知识运用.一生展示,其它小组补充完善,展示问题解决的方法,注重一题多解及解题过程中的共性问题,教师注意总结问题的深度和广度.甲小华乙ACBDE直击中考1.在和中,,如果的周长是16,面积是12,那么的周长、面积依次为()A.8,3B.8,6C.4,3D.4,62.(吉林省)如图,⊙o中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.(1)求证:;(2)当时,求的值3.(湖北孝感)如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是.教师展示问题,学生有针对性独立思考解答,完成后师生间展评.完善整合相似三师生梳理本课的知识点及及注意问——归结本节课所复习的内容,梳理知识,构建思维导图,凸显数学对内容的升华理解认识OFDAEBC知识框架相似三角形的性质性质方法的应用角形的性质:1.相似三角形对应高的比,对应中线的比与对应平分线的比都等于相似比.2.相似三角形对应线段的比等于相似比.3.相似三角形周长的比等于相似比4.相似三角形面积的比等于相似比的平方.你收获了什么?思想方法.生反思总结本课中的难点、重点及易错点,并在错题中整理所产生的问题.针对性问题师板书.作业必做题1.已知:如图,△ABC中,D在AC上,且AD:DC=1:2,E为BD的中点,AE的延长线交BC于F,求证:BF:FC=1:3选做题2.如图,矩形中,厘米,厘米().动点同时从点出发,分别沿,运动,速度是厘米/秒.过作直线垂直于,分别交,于.当点到达终点时,点也随之停止运动.设运动时间为秒.(1)若厘米,秒,则______厘米;(2)若厘米,求时间,使,并求出它们的相似比;(3)若在运动过程中,存在某时...