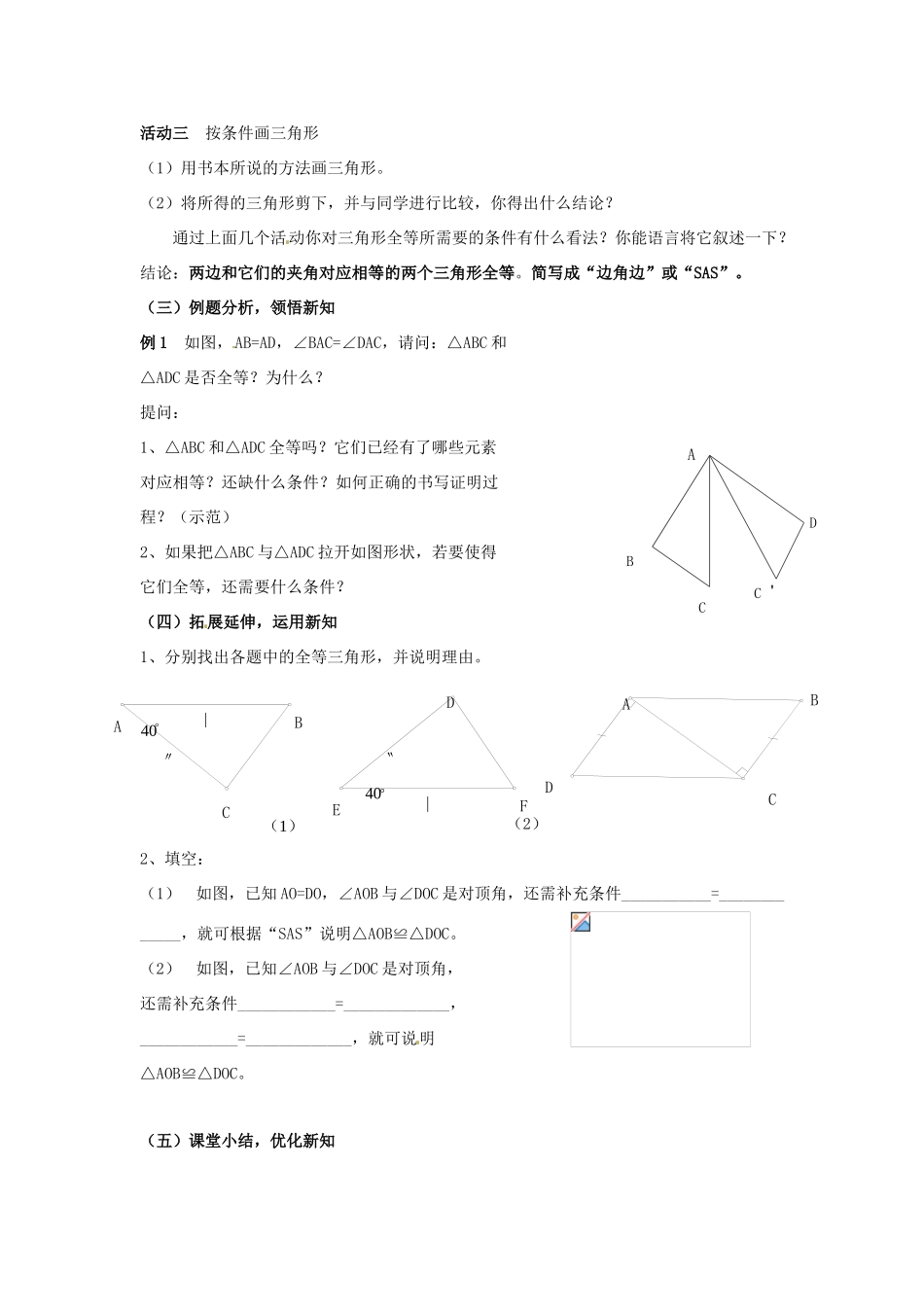
11.3探索三角形全等的条件(第一课时)一、教学目标:1、让学生懂得三角形全等必须具备三个条件理解“边角边”公理,学会用它来判定两个三角形全等。2、让学生学会有条理地思考、分析、解决问题的能力,培养学生推理、应用能力和空间想象能力。3、让学生学会大胆探索、善于归纳、应用、培养学生个性,优化学生数学思维品质。二、教学重难点:重点:掌握三角形全等的“边角边”条件。难点:正确运用“边角边”条件判定三角形全等,解决实际问题。三、教学方法:引导探索法,讲练结合,探索交流。四、教学过程:(一)创设情境,感悟新知复习:(1)如果两个三角形全等,那么它们的对应边和对应角有什么关系?(2)两个三角形需要具备什么条件,即它们有多少组边或角分别相等时就全等?提问:(1)当两个三角形只有1组边或角相等时,它们全等吗?(2)当两个三角形只有2组边或角相等时,它们全等吗?(3)当两个三角形有3组边或角相等时,它们全等吗?讨论:从三角形的6个元素中任意选出其中的3个元素,共有多少种不同的选法?(二)探索活动,揭示新知活动一P139做一做(1)任意剪一个直角三角形,同学们得到的三角形全等吗?(2)重新剪一个直角三角形,要使得全班同学剪下的都全等,你能做到吗?说说看(3)剪下直角三角形,验证并得出结论。活动二猜想、测量、验证(1)用仿照书本第137页的图12-7给出的几个三角形的图片,请学生先猜想:哪两个三角形全等?(2)验证你的猜想。DABC活动三按条件画三角形(1)用书本所说的方法画三角形。(2)将所得的三角形剪下,并与同学进行比较,你得出什么结论?通过上面几个活动你对三角形全等所需要的条件有什么看法?你能语言将它叙述一下?结论:两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”。(三)例题分析,领悟新知例1如图,AB=AD,∠BAC=∠DAC,请问:△ABC和△ADC是否全等?为什么?提问:1、△ABC和△ADC全等吗?它们已经有了哪些元素对应相等?还缺什么条件?如何正确的书写证明过程?(示范)2、如果把△ABC与△ADC拉开如图形状,若要使得它们全等,还需要什么条件?(四)拓展延伸,运用新知1、分别找出各题中的全等三角形,并说明理由。(2)2、填空:(1)如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件___________=_____________,就可根据“SAS”说明△AOB≌△DOC。(2)如图,已知∠AOB与∠DOC是对顶角,还需补充条件____________=_____________,____________=_____________,就可说明△AOB≌△DOC。(五)课堂小结,优化新知C'DCBA(1)40°〃∣CAB40°∣〝DEFADCB1、经历了剪纸、测量、画图等方法探索三角形全等的活动过程,积累了数学活动经验。2、归纳得出了两个三角形全等的条件—“SAS”,知道了有两边和其中一边的对角对应相等的两个三角形不一定全等,初步发展了推理能力。(六)布置作业P151习题11.31、3