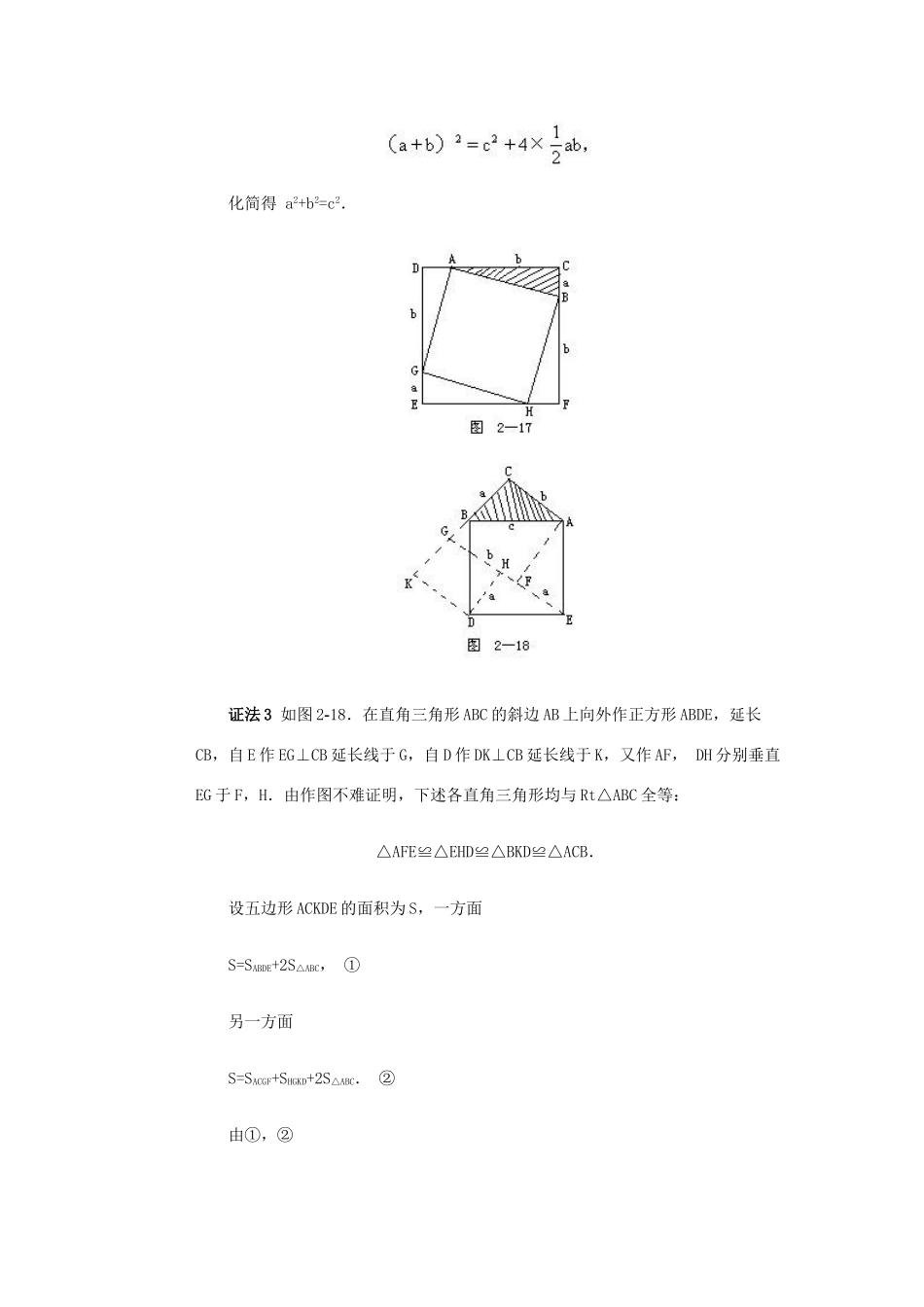
第三十二讲勾股定理与应用在课内我们学过了勾股定理及它的逆定理.勾股定理直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2.勾股定理逆定理如果三角形三边长a,b,c有下面关系:a2+b2=c2那么这个三角形是直角三角形.早在3000年前,我国已有“勾广三,股修四,径阳五”的说法.关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法1是欧几里得证法.证法1如图2-16所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.下面证明,大正方形的面积等于两个小正方形的面积之和.过C引CM∥BD,交AB于L,连接BG,CE.因为AB=AE,AC=AG,∠CAE=∠BAG,所以△ACE≌△AGB(SAS).而所以SAEML=b2.①同理可证SBLMD=a2.②①+②得SABDE=SAEML+SBLMD=b2+a2,即c2=a2+b2.证法2如图2-17所示.将Rt△ABC的两条直角边CA,CB分别延长到D,F,使AD=a,BF=b.完成正方形CDEF(它的边长为a+b),又在DE上截取DG=b,在EF上截取EH=b,连接AG,GH,HB.由作图易知△ADG≌△GEH≌△HFB≌△ABC,所以AG=GH=HB=AB=c,∠BAG=∠AGH=∠GHB=∠HBA=90°,因此,AGHB为边长是c的正方形.显然,正方形CDEF的面积等于正方形AGHB的面积与四个全等的直角三角形(△ABC,△ADG,△GEH,△HFB)的面积和,即化简得a2+b2=c2.证法3如图2-18.在直角三角形ABC的斜边AB上向外作正方形ABDE,延长CB,自E作EG⊥CB延长线于G,自D作DK⊥CB延长线于K,又作AF,DH分别垂直EG于F,H.由作图不难证明,下述各直角三角形均与Rt△ABC全等:△AFE≌△EHD≌△BKD≌△ACB.设五边形ACKDE的面积为S,一方面S=SABDE+2S△ABC,①另一方面S=SACGF+SHGKD+2S△ABC.②由①,②所以c2=a2+b2.关于勾股定理,在我国古代还有很多类似上述拼图求积的证明方法,我们将在习题中展示其中一小部分,它们都以中国古代数学家的名字命名.利用勾股定理,在一般三角形中,可以得到一个更一般的结论.定理在三角形中,锐角(或钝角)所对的边的平方等于另外两边的平方和,减去(或加上)这两边中的一边与另一边在这边(或其延长线)上的射影的乘积的2倍.证(1)设角C为锐角,如图2-19所示.作AD⊥BC于D,则CD就是AC在BC上的射影.在直角三角形ABD中,AB2=AD2+BD2,①在直角三角形ACD中,AD2=AC2-CD2,②又BD2=(BC-CD)2,③②,③代入①得AB2=(AC2-CD2)+(BC-CD)2=AC2-CD2+BC2+CD2-2BC·CD=AC2+BC2-2BC·CD,即c2=a2+b2-2a·CD.④(2)设角C为钝角,如图2-20所示.过A作AD与BC延长线垂直于D,则CD就是AC在BC(延长线)上的射影.在直角三角形ABD中,AB2=AD2+BD2,⑤在直角三角形ACD中,AD2=AC2-CD2,⑥又BD2=(BC+CD)2,⑦将⑥,⑦代入⑤得AB2=(AC2-CD2)+(BC+CD)2=AC2-CD2+BC2+CD2+2BC·CD=AC2+BC2+2BC·CD,即c2=a2+b2+2a·cd.⑧综合④,⑧就是我们所需要的结论特别地,当∠C=90°时,CD=0,上述结论正是勾股定理的表述:c2=a2+b2.因此,我们常又称此定理为广勾股定理(意思是勾股定理在一般三角形中的推广).由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响.在△ABC中,(1)若c2=a2+b2,则∠C=90°;(2)若c2<a2+b2,则∠C<90°;(3)若c2>a2+b2,则∠C>90°.勾股定理及广勾股定理深刻地揭示了三角形内部的边角关系,因此在解决三角形(及多边形)的问题中有着广泛的应用.例1如图2-21所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.分析注意到正方形的特性∠CAB=45°,所以△AGF是等腰直角三角形,从而有AF2=2FG2,因而应有AF=AB,这启发我们去证明△ABE≌△AFE.证因为AE是∠FAB的平分线,EF⊥AF,又AE是△AFE与△ABE的公共边,所以Rt△AFE≌Rt△ABE(AAS),所以AF=AB.①在Rt△AGF中,因为∠FAG=45°,所以AG=FG,AF2=AG2+FG2=2FG2.②由①,②得AB2=2FG2.说明事实上,在审题中,条件“AE平分∠BAC”及“EF⊥AC于F”应使我们意识到两个直角三角形△AFE与△ABE全等,从而将AB“过渡”到AF,使AF(即AB)与FG处于同一个直角三角形中,可以利用勾股定理进行证明了.例2如图2-22所示.AM是△ABC的BC边上的中线,求证:AB2+AC2...