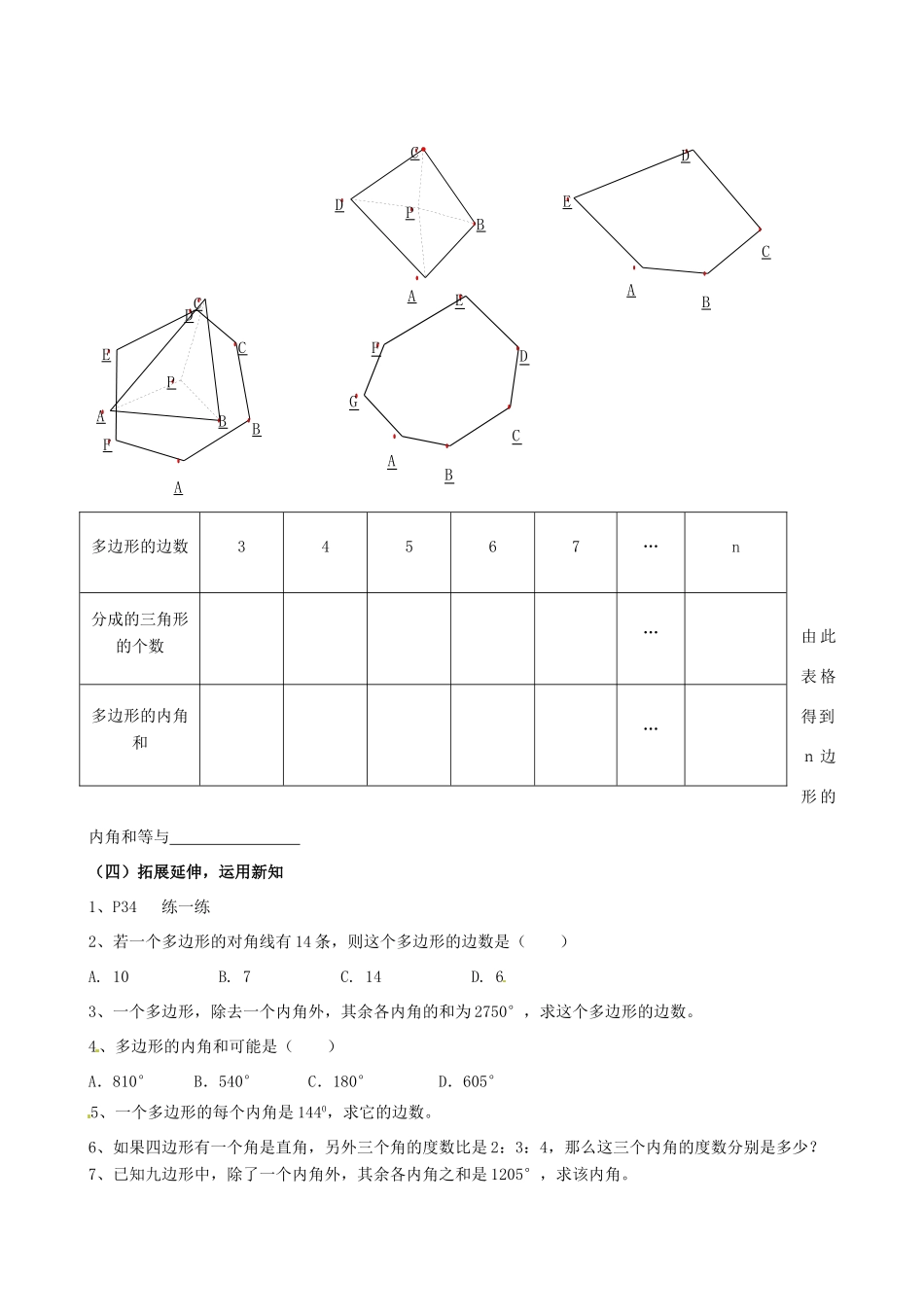
C7.5三角形的内角和(第二课时)一、教学目标:1、通过将多边形分割成三角形,从而探索出多边形内角和的计算公式,并能进行应用。2、经历操作、观察、探索等活动,进一步提高学生分析问题、解决问题的水平,提升从不同角度思考问题的能力。3、通过交流,学会合作。二、教学重难点:重点:探索多边形内角和的计算公式,并能进行应用。难点:从不同角度思考问题。三、教学方法:引导探索法,讲练结合,探索交流。四、教学过程:(一)创设情境,感悟新知1、在△ABC中,(1)∠C=90º,∠B=30º,则∠A=;(2)∠A=100º,∠B=∠C,则∠B=;(3)∠B=30º,∠C=2∠A,则∠C=;(4)∠A:∠B:∠C=2:3:4,则∠A=;∠B=;∠C=。2、三角形的内角和是180°,多边形的内角和如何计算呢?你知道四边形的内角和吗?在小学计算不规则多边形的面积大多采用什么方法?(回忆小学所学内容,为学习新知识作铺垫。通过提问,激发学生探索多边形内角和的欲望。)(二)动手操作,探索体验1、如图,连接AC,把四边形ABCD分成2个三角形,你能计算四边形ABCD的内角和吗?四边形ABCD的内角和是180°×2=360°。2、如图,把五边形ABCDE分成3个三角形,你能计算五边形ABCDE的内角和吗?EDBDA五边形ABCDE的内角和是180°×3=540°。3、仿照上面的方法,六边形ABCDEF可以分成多少个三角形?n边形可以分成多少个三角形?填表:多边形边数456…n分成的三角形个数234…多边形的内角和180°×2180°×3180°×4…由此表格得到,n边形的内角和等与1、想一想:你还有不同于上述的分割方案吗?(分组讨论,启发学生从不同角度思考问题)(1)用如下所示的分法,将多边形分割成三角形,并完成表格:CBA由此表格得到n边形的内角和等与(四)拓展延伸,运用新知1、P34练一练2、若一个多边形的对角线有14条,则这个多边形的边数是()A.10B.7C.14D.63、一个多边形,除去一个内角外,其余各内角的和为2750°,求这个多边形的边数。4、多边形的内角和可能是()A.810°B.540°C.180°D.605°5、一个多边形的每个内角是1440,求它的边数。6、如果四边形有一个角是直角,另外三个角的度数比是2:3:4,那么这三个内角的度数分别是多少?7、已知九边形中,除了一个内角外,其余各内角之和是1205°,求该内角。多边形的边数34567…n分成的三角形的个数…多边形的内角和…_C_A_B_P_E_D_C_B_A_F_E_D_C_B_A_D_A_B_C_P_F_E_D_C_B_A_G(通过练习,让学生内化知识)六)布置作业P37习题7.52