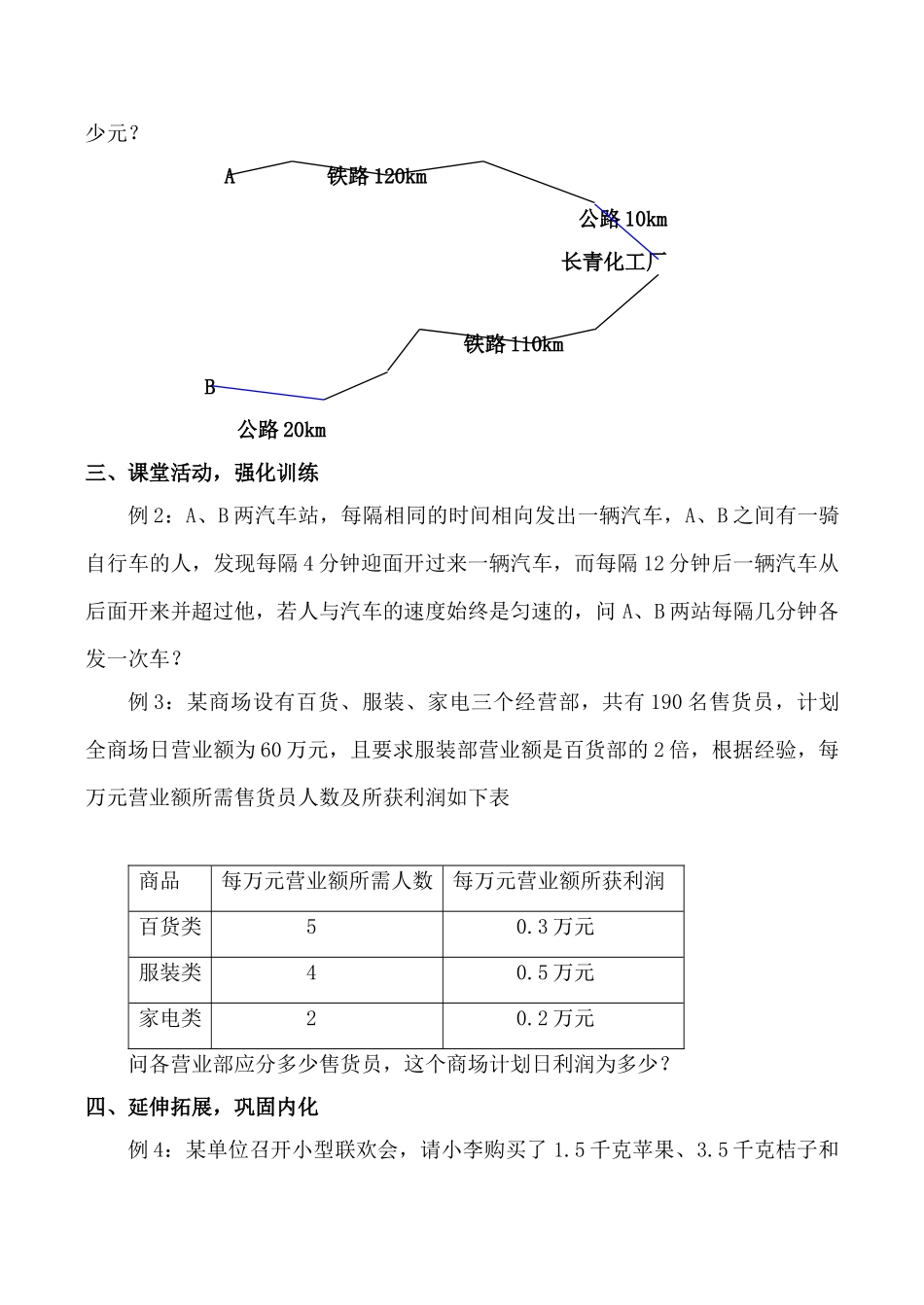
再探实际问题与二元一次方程组(第3课时)★目标预设一、知识与能力充分理清实际问题与二元一次方程组之间的联系,能熟练运用方程组来解决有关实际问题。二、过程与方法会将实际问题转化为数学模型,通过列方程组解决问题,进一步了解用方程组解决实际问题的基本过程,体会数学的应用价值。三、情感、态度、价值观在独立思考的基础上,积极参与讨论,敢于发表自己的观点并尊重与理解他人的见解,能从交流中获得知识。★教学重难点一、重点:熟练运用列方程组解决实际问题二、难点:正确通过分析、总结列方程组★教学准备:小黑板,关于增长率的实际问题若干★预习导学:某厂2000年的总产值比总支出多600万元,2001年加强和改革了内部管理,结果总产值上升15%,总支出下降了5%,总产值比总支出多750万元,求该厂2001年的总支出和总产值。★教学过程一、创设情景,谈话导入我们前面几节研究了一些实际问题,由以上探究可以看出,方程组是解决含有多个未知数的重要工具,列出方程组要根据问题中的数量关系,解出方程组的解后,应进一步考虑它是否符合问题的实际意义。二、精讲点拔,质疑问难例1:如图,长青化工厂与A、B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运往B地,公路运价为1.5元/吨·千米,铁路运价为1.2元/吨·千米,这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?A铁路120km公路10km长青化工厂铁路110kmB公路20km三、课堂活动,强化训练例2:A、B两汽车站,每隔相同的时间相向发出一辆汽车,A、B之间有一骑自行车的人,发现每隔4分钟迎面开过来一辆汽车,而每隔12分钟后一辆汽车从后面开来并超过他,若人与汽车的速度始终是匀速的,问A、B两站每隔几分钟各发一次车?例3:某商场设有百货、服装、家电三个经营部,共有190名售货员,计划全商场日营业额为60万元,且要求服装部营业额是百货部的2倍,根据经验,每万元营业额所需售货员人数及所获利润如下表商品每万元营业额所需人数每万元营业额所获利润百货类50.3万元服装类40.5万元家电类20.2万元问各营业部应分多少售货员,这个商场计划日利润为多少?四、延伸拓展,巩固内化例4:某单位召开小型联欢会,请小李购买了1.5千克苹果、3.5千克桔子和0.5千克瓜子,共用了16.30元。后因故又请小李按原价增购了2千克苹果,5千克桔子和0.5千克瓜子,又用了21.80元。另有一位顾客按小李的购货价购买了苹果、桔子、瓜子各0.5千克,营业员收货款5.80元,小李经过思考后发现营业员算帐有了差错,请你算一下,是否有错?如有错,是多收了还是少收了顾客的款?例5:一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用。已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运这批货物分别用2a次、a次能运完;若甲、丙两车合运相同次数运完这批货物时,甲车共运了180吨;若乙、丙两车合运相同次数运完这批货物时,乙车共运了270吨。问:(1)乙车每次所运货物量是甲车每次所运货物量的几倍?(2)现甲、乙、丙合运相同次数,把这批货物运完时,货主应付车主运费各多少元?(按每运用1吨运费20元计算)