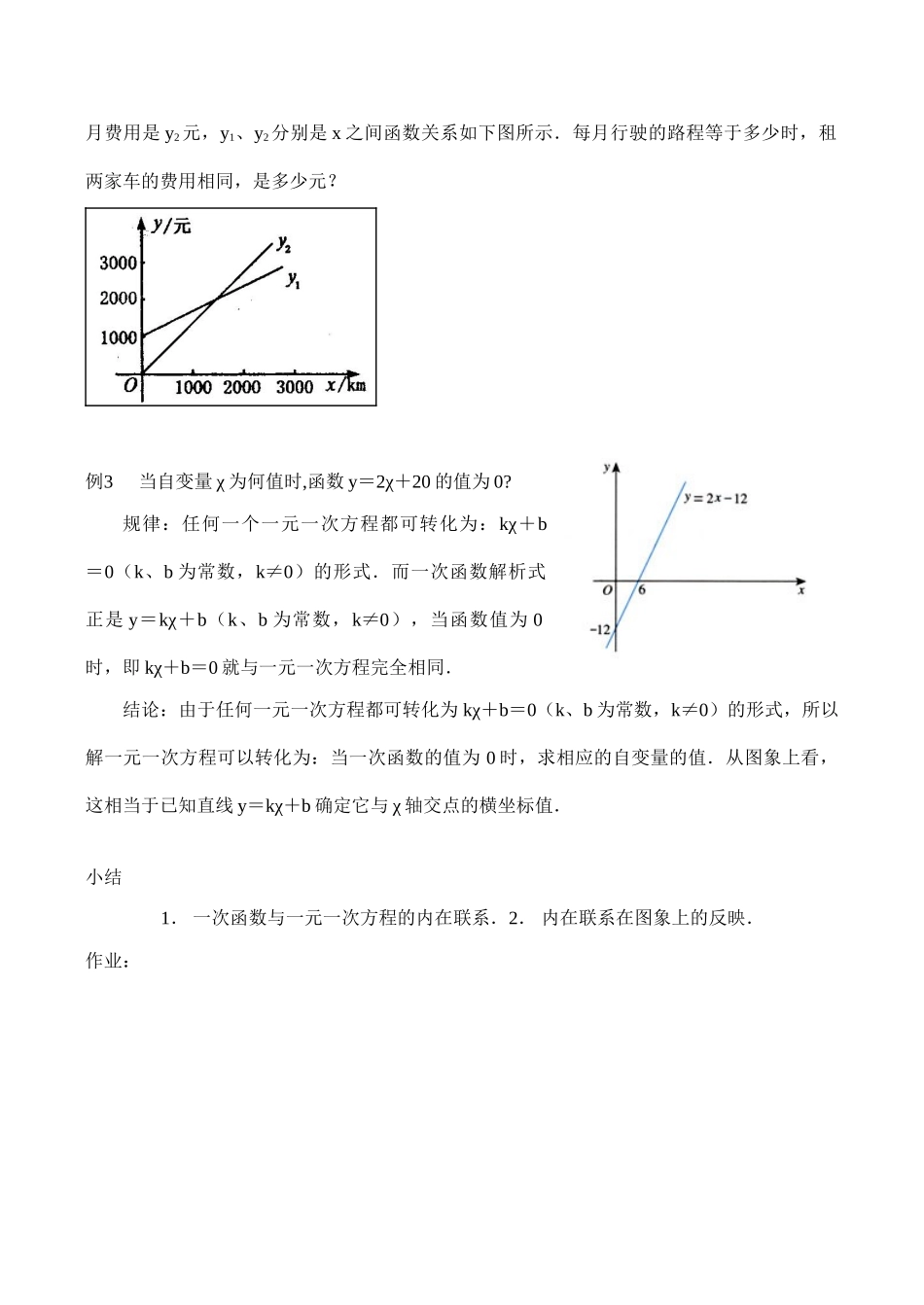
八年级数学一次函数与一元一次方程教学目标:理解一元一次方程与函数图像之间的关系,会用图象法解一元一次方程.加深理解数形结合思想.重点:1.函数观点认识一元一次方程.2.应用函数求解一元一次方程.难点:用函数观点认识一元一次方程.教学过程:一.复习提问一次函数y=kx+b图像的形状是一条直线.二.讲解:1.方程2x+20=02.函数y=2x+20观察思考:二者之间有什么联系?从数上看:方程2x+20=0的解,是函数y=2x+20的值为0时,对应自变量的值从形上看:函数y=2x+20与x轴交点的横坐标即为方程2x+20=0的解关系:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.例1一个物体现在的速度是5m/s,其速度每秒增加2m/s,再过几秒它的速度为17m/s?(用两种方法求解)例2利用图象求方程6x-3=x+2的解练习:用不同种方法解下列方程:1.2x-3=x-2.2.x+3=2x+1.3.某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司其中一家签让合同.设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费用是y2元,y1、y2分别是x之间函数关系如下图所示.每月行驶的路程等于多少时,租两家车的费用相同,是多少元?例3当自变量χ为何值时,函数у=2χ+20的值为0?规律:任何一个一元一次方程都可转化为:kχ+b=0(k、b为常数,k≠0)的形式.而一次函数解析式正是у=kχ+b(k、b为常数,k≠0),当函数值为0时,即kχ+b=0就与一元一次方程完全相同.结论:由于任何一元一次方程都可转化为kχ+b=0(k、b为常数,k≠0)的形式,所以解一元一次方程可以转化为:当一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线у=kχ+b确定它与χ轴交点的横坐标值.小结1.一次函数与一元一次方程的内在联系.2.内在联系在图象上的反映.作业: