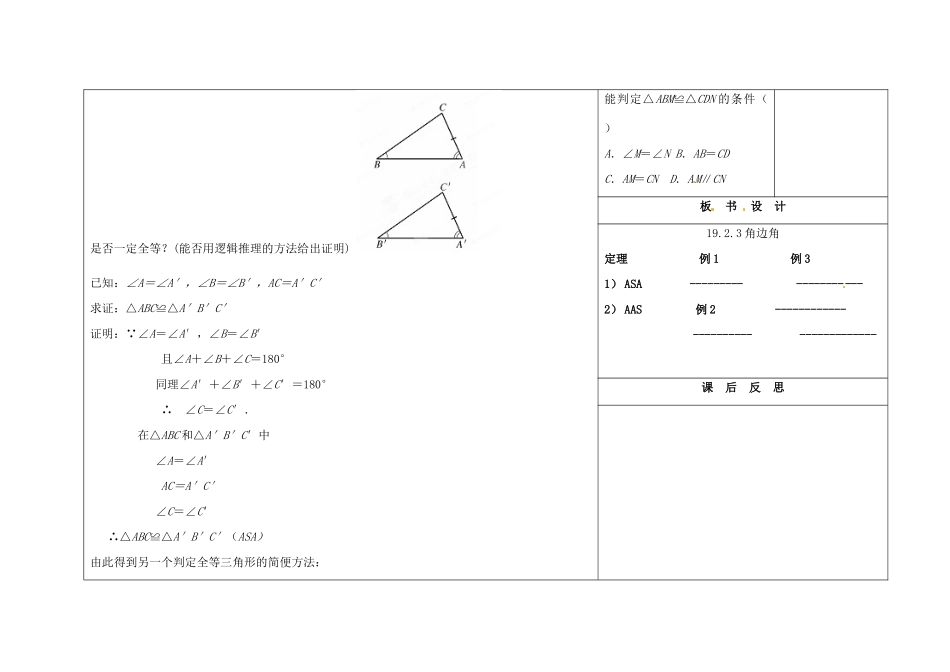
课题19.2.3角边角课型新课总节时教学目标知识目标:使学生理解ASA的内容,能运用ASA全等判定法来判定三角形全等进而说明线段或角相等;能力目标:通过画图、实验、发现、应用的过程教学,树立学生知识源于实践用于实践的观念;情感目标:使学生体会探索发现问题的过程.经历自己探索出AAS的三角形全等判定及其应用.重点利用三角形全等的判定法,间接说明角相等或线段相等.难点三角形全等的判定法ASA和AAS及应用.教学过程差异个性设计教学资源创设情境前面,我们已经知道,当两个三角形的两条边及其夹角分别对应相等时,两个三角形一定全等。而当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形未必一定全等。现在,讨论相对的情况:如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?那么有几种可能的情况呢?(一种情况是两个角及两角的夹边;另一种情况是两个角及其中一角的对边.)每一种情况下得到的三角形都全等吗?补充例题例2、如图,已知∠1=∠2,∠C=∠D。求证:AC=AD探究归纳1.请同学们动手做一个实验:六位同学为一组.(1)共同商定画出任意一条线段AB,与两个角、()(2)同学各自在硬纸板上画线段的长等于商定的线段AB的长,在的同旁,画等于商定的,画等于商定的,设与相交于,便得△.(3)用剪刀各自剪出△,将同组同学剪出的两个三角形重叠在一起发现了什么?其他组的同学是否也有同样的结论呢?同学们各抒己见后,总结:对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.由此得到另一个判定全等三角形的简便方法:如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简记为“角边角”或简记为(A.S.A.).[2.思考:如图,如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形例3、如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由变式1:若AD、BE改为分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由.变式2:若AD、BE改为分别是两腰上的高,△ABD和△BAE全等吗?试说明理由.合作运用先独立思考,再小组讨论交流.已知MB=ND,∠1=∠2,下列不是否一定全等?(能否用逻辑推理的方法给出证明)已知:∠A=∠A′,∠B=∠B′,AC=A′C′求证:△ABC≌△A′B′C′证明:∵∠A=∠A′,∠B=∠B′且∠A+∠B+∠C=180°同理∠A′+∠B′+∠C′=180°∴∠C=∠C′.在△ABC和△A′B′C′中∠A=∠A′AC=A′C′∠C=∠C′∴△ABC≌△A′B′C′(ASA)由此得到另一个判定全等三角形的简便方法:能判定△ABM≌△CDN的条件()A.∠M=∠NB.AB=CDC.AM=CND.AM∥CN板书设计19.2.3角边角定理例1例31)ASA--------------------2)AAS例2-----------------------------------课后反思如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.简写成:“角角边”或简记为(AAS).实践应用例1、如图,,,求证:△ABC≌△DCB证明:已知,又BC是公共边,由(ASA)全等判定法,可知△ABC≌△DCB检测反馈教材79页习题3交流反思本节课你学到了什么知识,对这些知识有什么体会,对本节的知识存在着哪些疑问?差异作业