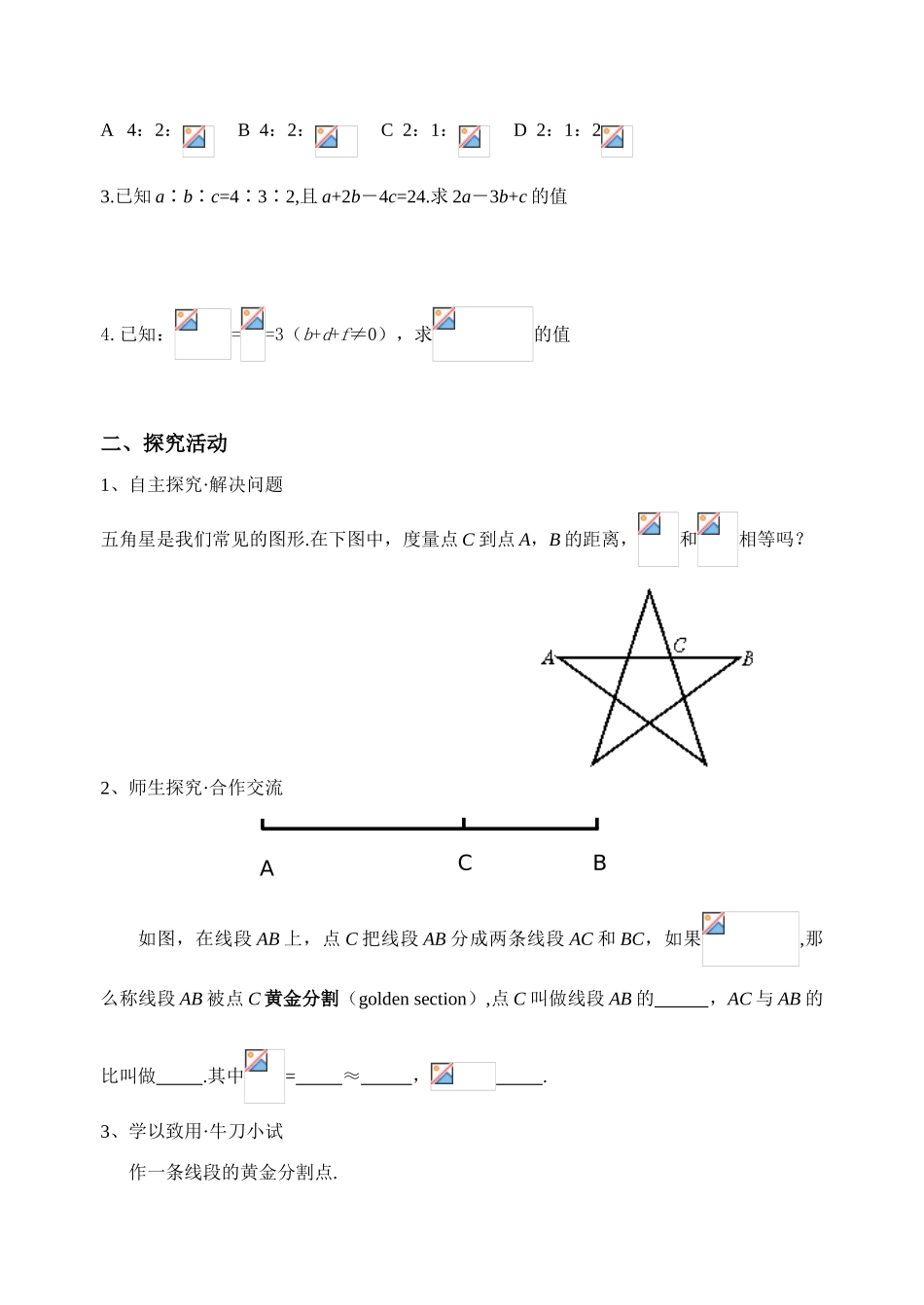
大路中学数学讲学稿学习目标1、掌握黄金分割的含义.2、能通过作图找到一条线段的黄金分割点.学习重点能通过作图找到一条线段的黄金分割点.学习难点掌握黄金分割的含义并能进行简单运用.一、学前准备1.填空(1)四条线段a,b,c,d中,如果a与b的比等于c与d的比,即(或a:b=c:d)那么这四条线段a,b,c,d叫做,简称.反过来,如果四条线段a,b,c,d成比例线段,则可以记作.(2)已知a=2,b=4,c=6;若a,b,c,x是成比例线段,则x=;若a,x,b,c是成比例线段,则x=.(3)若则;;;(4)小明的身高为1.6m,测得他的影长为1m,在同一时刻,旗杆的影长为5m,则旗杆的实际高度是.2.选择(1)已知,则把它改写成比例式后错误的是()ABCD(2)一个矩形的长为2cm,宽为1cm,则它的长、宽及对角线的比为()A4:2:B4:2:C2:1:D2:1:23.已知a∶b∶c=4∶3∶2,且a+2b-4c=24.求2a-3b+c的值4.已知:==3(b+d+f≠0),求的值二、探究活动1、自主探究·解决问题五角星是我们常见的图形.在下图中,度量点C到点A,B的距离,和相等吗?2、师生探究·合作交流如图,在线段AB上,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割(goldensection),点C叫做线段AB的,AC与AB的比叫做.其中=≈,.3、学以致用·牛刀小试作一条线段的黄金分割点.ACB如图,已知线段AB,按照如下方法作图:(1)经过点B作BD⊥AB,使BD=AB.(2)连接AD,在DA上截取DE=DB.(3)在AB上截取AC=AE.则点C为线段AB的黄金分割点.你知道为什么吗?线段AB有没有除点C以外的黄金分割点呢?如果有应满足怎样的条件?三、自我测验1、选择(1)已知线段AB的黄金分割点是C,且AC>BC,则下列各式正确的是()A.AB2=AC·CBB.CB2=AC·ABC.AC2=CB·ABD.AC2=2AB·BC(2)若AB=a,C点是AB上的黄金分割点,且AC>BC,则BC等于()A.B.C.1D.无法判断(3)若点C为线段AB的黄金分割点,则等于()A.B.C.或D.2、填空(1)已知点C为线段AB的黄金分割点,且=,则的近似值为(2)点C是线段AB上的一个黄金分割点,且AC>BC,若AB=5cm,则AC=_____,BC=____.(3)若点C是线段AB上一点,AB=1,AC=,则AC:BC=______.(4)把长为10cm的线段黄金分割,则较长的线段长为;较短的线段长为.(结果精确到0.01)四、学习收获1、通过今天的学习,你有何收获?2、预习中遇到困惑解决了吗?3、你还有哪些疑惑?五、应用与拓展1、如图,点C,D是线段AB的两个黄金分割点,已知AB=1,试求CD的长2、作图(1)宽与长的比等于黄金比的矩形称为黄金矩形.设法做出一个黄金矩形(2)底边与腰的比等于黄金比的等腰三角形称为黄金三角形,设法做出一个黄金三角形3、收集一些有关黄金分割的数学知识,例如黄金分割的由来、黄金分割在实际生活中的运用等等,介绍给你的同伴.