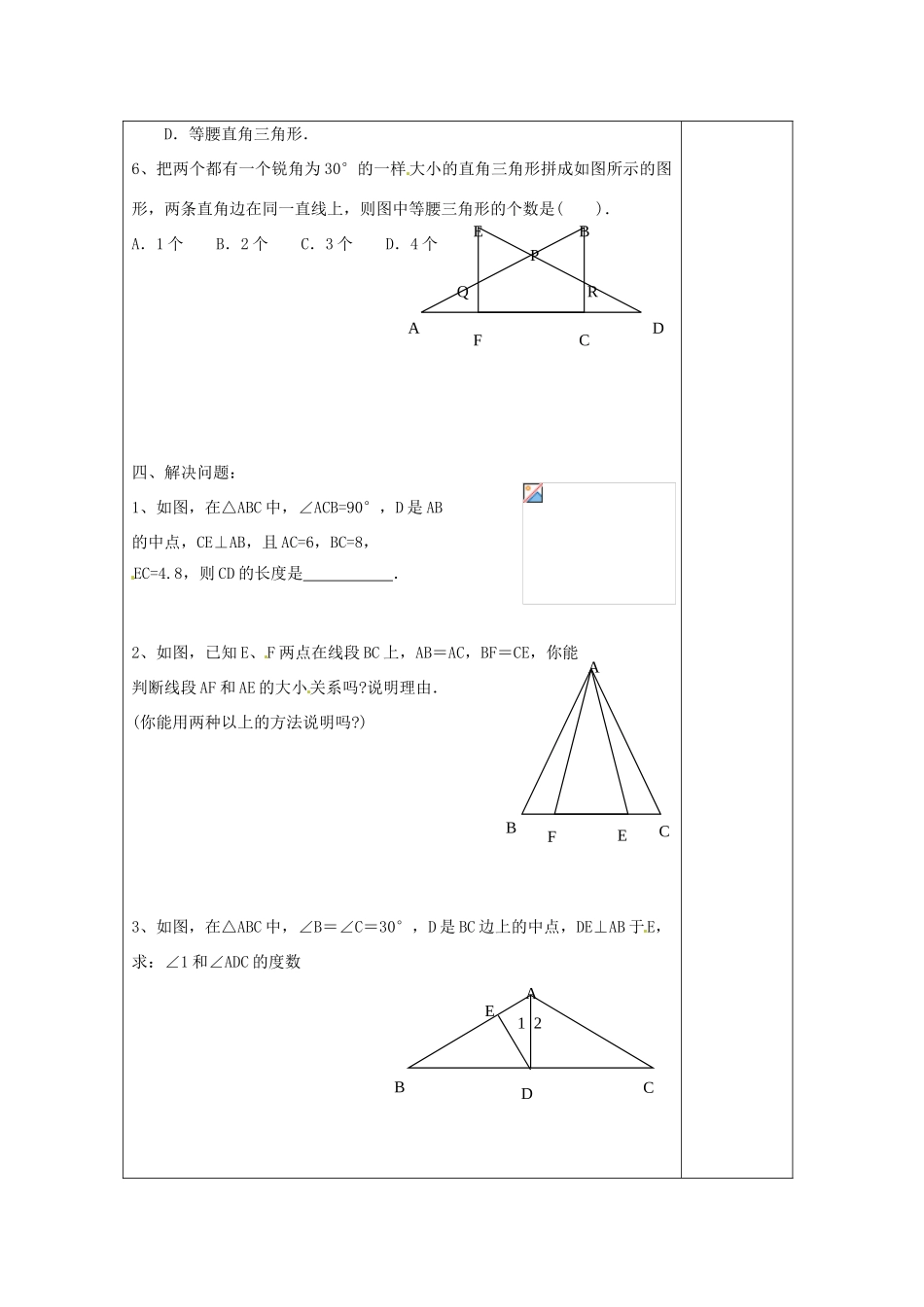
江苏省涟水县徐集中学八年级数学上册第一章轴对称图形1.5等腰三角形的轴对称性教案2苏科版教学方法教学过程教学活动内容个人主页一、情景创设:1.前面探索了等腰三角形的一个重要性质:如果有两条边相等,那么这两条边所对的角相等。反过来,在一个三角形中,如果有两个角相等,那么这两个角所对的边的大小有什么关系?二、新知探究1、如图,∠1=∠2,∠3=∠4,猜想PM、PN、QM、QN之间的大小关系,并测量各个线段的长,验证你的猜想.还可以利用课本上的在长方形纸条上画直线折叠的方法进行验证2、引导学生用比较准确的语言叙述所得到的结论:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”)符号语言:如图,在△ABC中,若∠B=∠C,则AB=AC.3、折直角三角形纸片按照课本上设计的步骤组织学生折直角三角形纸片时,教师引导学生把“操作和思考有机的结合起来”,把学生的兴趣引导到发现规律上来,如果学生探索结论有困难,教学中可适当设计不同的问题让学生回答,ABCEFO如:D是斜边AB的中点吗?为什么?图中有哪些相等的角?有几个等腰三角形?哪些相等的线段?得出结论:直角三角形斜边上的中线等于斜边的一半符号语言:如图,在△ABC中,∠ACB=90°,因为AD=BD(或者D为AB中点),所以三、尝试运用:1、例题1(课本P25例2):在△ABC中,AB=AC,角平分线BD、CE相交与点O,OB与OC相等吗?请说明理由.解答这个题目时,可引导学生分析:OB=OC应该具备什么条件?题目中的条件是否可以转化成所需要的条件?如何进行转化?2、△ABC中,角平分线BO与CO的相交点O,OE∥AB,OF∥AC,BC=10,求△OEF的周长.3、学生完成练习:P261、2、34、给出下面四个条件:①已知两腰;②已知底边和顶角;③已知顶角和底角;④已知底边和底边上的高.其中能确定一个等腰三角形的大小、形状的条件有().A、1个B、2个C、3个D、4个5、一个三角形的三个外角的度数之比5:4:5,那么这个三角形是()A.等腰三角形,但不是等边三角形,也不是等腰直角三角形B.等边三角形C.直角三角形,但不是等腰三角形D.等腰直角三角形.6、把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上,则图中等腰三角形的个数是().A.1个B.2个C.3个D.4个四、解决问题:1、如图,在△ABC中,∠ACB=90°,D是AB的中点,CE⊥AB,且AC=6,BC=8,EC=4.8,则CD的长度是.2、如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.(你能用两种以上的方法说明吗?)3、如图,在△ABC中,∠B=∠C=30°,D是BC边上的中点,DE⊥AB于E,求:∠1和∠ADC的度数AEBPQRCDFABCFEABCDE12五、课堂小结:这节课你有什么收获?1、探究得到了判定一个三角形是等腰三角形的条件以及“直角三角形斜边上的中线等于斜边的一半”这个性质,在应用这些结论解决问题过程中进一步提高了说理、分析、识图和归纳的能力六、作业设计:课本P29习题1.5第6、7、8题教学反思